Electronic Properties of Metallic Heterostructures
Surface states on close-packed surfaces of noble metals
The noble metals gold, silver, and copper have a surface state at their (111)-surfaces. Electrons in these states are confined near the surface, but can move freely parallel to the surface. (They can be characterized as a two-dimensional electron gas.)
If these electrons hit a defect (e.g. a surface step or a chemical impurity), they are partially reflected. Around these defects, incoming and outgoing waves interfere and form a standing wave pattern.
The resulting variations in the local density of states are analyzed by measuring the thermovoltage in a scanning tunneling microscope.
Surface state at gold(111): Influence of the herringbone reconstruction

The herringbone reconstruction of the (111) oriented gold surface can be identified by double rows forming a zigzag pattern.
The distance between bends equals four times the wavelength of the analyzed electrons.
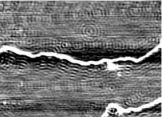
If every bend acts as a scattering center for the electrons, standing waves from neighboring bends interfere constructively. Therefore there are strong standing waves along the bends.
Influence of adsorbates on the surface state
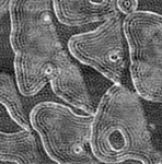
The wave functions of surface state electrons spread into the substrate for several atomic distances. Nonetheless a single layer of adsorbate atoms changes the fermi wavelength of the electrons.
The thermovoltage is different for chemically different atoms. This makes it easy to distinguish between the clean surface and the deposited material.
Temperature dependence of the mean free path of electrons in surface states
The amplitude of the standing wave pattern decays with increasing distance to the step. The decay length is affected by the mean free path of the electrons: The shorter the mean free path, the faster the wave patterns disappear. The mean free path of the electrons is determined by comparing the thermovoltage image with model calculations.
