Elektronische Eigenschaften von Heterostrukturen

Oberflächenzustände auf dichtgepackten Edelmetalloberflächen

Die Edelmetalle Gold, Silber und Kupfer besitzen auf ihren (111)-Oberflächen einen elektronischen Zustand, in dem Elektronen auf einen Bereich nahe der Festkörperoberfläche beschränkt sind. Parallel zur Festkörperoberfläche können sie sich jedoch frei bewegen. (Man spricht von einem zweidimensionalen Elektronengas.)

Wenn diese Elektronen auf eine Störung treffen (z.B. eine Stufe des Festkörpers oder eine punktförmige Fehlstelle), können sie reflektiert werden. Wegen des Wellencharakters der Elektronen bilden sich dann stehende Wellen um die Störstellen aus.

Diese Variationen der elektronischen Zustandsdichte untersuchen wir mithilfe der Thermospannung.

Einfluss der Rekonstruktion von Gold(111) auf den Oberflächenzustand

Fig.1: Topographie der Goldoberfläche: Ober- und unterhalb einer Stufe erkennt man die Rekonstruktion.

Die Rekonstruktion der Goldoberfläche liefert auffällige Doppelreihen, die nach einer gewissen Strecke die Richtung um 60° wechseln. Der Abstand der Knicke voneinander entspricht der vierfachen Wellenlänge der untersuchten Elektronen.

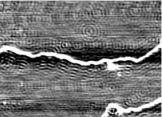
Fig. 2: Thermospannung: stehende Wellen an der Stufe, an Verunreinigungen und entlang der Knicke.

Wenn nun jeder Knick als Streuzentrum für die Oberflächenzustände wirkt, interferieren die Wellen benachbarter Knicke konstruktiv miteinander, es gibt also besondere stehende Wellen entlang der Knicke.

Veränderung des Oberflächenzustands durch Adsorbate

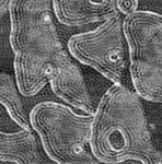
Fig. 3: Thermospannung von gut 1/2 ML Silber (hell) auf Gold (dunkel)

Die Wellenfunktionen der Oberflächenzustände dehnen sich über einige Atomlagen in den Festkörper hinein aus. Dennoch beeinflusst schon eine Monolage (ML) eines anderen Materials die Fermi-Wellenlänge.

Die Thermospannung liefert auch einen Kontrast zwischen den verschiedenen Materialien, sodass man die unbedeckte Oberfläche und die aufgewachsenen Materialien einfach voneinander unterscheiden kann.

Temperaturabhängigkeit der mittleren freien Weglänge für Elektronen in Oberflächenzuständen

Die Länge, über die man an einer Kante stehende Wellen beobachten kann, wird unter anderem bestimmt durch die mittlere freie Weglänge der Elektronen. Je früher die Elektronen einen Stoß durchführen, desto schneller nehmen die stehenden Wellen ab. Durch Vergleich der aufgenommenen Bilder mit Modellrechnungen kann die mittlere freie Weglänge der Elektronen bestimmt werden.

Verzerrungsgitter beim Wachstum von Salz auf Silber(111) und Kupfer(111)

Fig. 4: dI/dV-Messungen von NaCl-Inseln auf Ag(111), die Verzerrungsgitter unterschiedlicher Periodizität und Orientierung gegenüber der Inselkanten zeigen. Kreiswellen resultieren aus Streuprozesse der Elektronen im Oberflächenzustand.

Das Wachstum von monoatomar dünnen Inseln aus Salz (NaCl) auf die (111)-Oberflächen der Edelmetalle Kupfer und Silber führt zu interessanten Effekten in der lokalen Oberflächenzustandsdichte, die durch STM-Messungen sichtbar gemacht werden können. Geometrisch betrachtet, passt die Kristallstruktur von Salz (kubisch) nicht ohne Weiteres auf die hexagonalen (111)-Oberflächen. Überschreitet die NaCl-Insel eine gewisse kritische Größe, führt das deshalb zur Ausbildung eines Verzerrungsgitters aus parallel angeordneten äquidistanten Reihen, die an ein Waschbrett erinnern. Die Periodizität und der Winkel der Reihen gegenüber den Inselkanten ist dabei sowohl von der Größe der NaCl-Insel als auch von der Ausrichtung gegenüber der Substratoberfläche abhängig. Die Abbildung 4 zeigt hierzu einige mit dem STM aufgenommene dI/dV-Messungen.

Veränderung des Oberflächenzustands durch Monolagen Salz

Wie oben erwähnt, besitzen auch die (111)-orientierten Oberflächen von Silber und Kupfer einen Oberflächenzustand. Dieser Oberflächenzustand „überlebt“ durch die sehr dünnen Lagen Salz hindurch als Grenzflächenzustand. Die Elektronen in diesem Zustand können ebenfalls als zweidimensionales Elektronengas behandelt werden, das an Defekten wie Stufenkanten oder Adsorbaten streut. Das dadurch gebildete stehende Wellenmuster kann durch Messung der differentiellen Leitfähigkeit direkt mit dem STM sichtbar gemacht werden. Es fällt auf, dass die Wellen auf der Salzinsel bei gleicher Energie eine andere Wellenlänge haben als die Wellen auf dem Substrat. Dies resultiert aus der energetischen Verschiebung des Grenzflächenzustands gegenüber dem Oberflächenzustands.

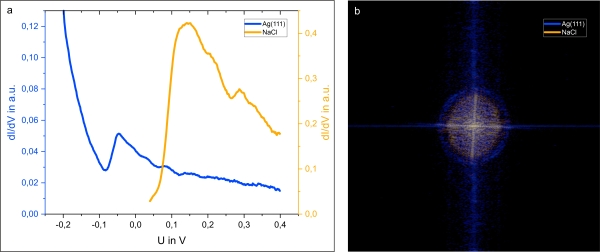
Im Falle des Rastertunnelmikroskops wird die Energie der Elektronen gerade durch die zwischen Spitze und Probe angelegte Tunnelspannung bestimmt. Wird diese kontinuierlich verändert und gleichzeitig die differentielle Leitfähigkeit aufgenommen, kann der Beginn des Oberflächen- und Grenzflächenzustands und ihre energetische Verschiebung zueinander ausgemessen werden (Fig. 5a). Um hingegen die Dispersionsrelation der Zustände bestimmen zu können, kann das Wellenmuster bei verschiedenen Tunnelspannungen aufgenommen und die resultierende Wellenlänge gegen die jeweilige Energie aufgetragen werden. Hieraus ergibt sich eine quadratische Abhängigkeit der Energie vom Wellenvektor. Zur Bestimmung der Wellenlänge kann der Übergang in den k-Raum nützlich sein, indem die Fouriertransformation des Bildes gebildet wird (Fig. 5b). Es ergeben sich durch die isotrop laufenden Wellen Kreise, deren Radius reziprok von der Wellenlänge abhängig ist. Entsprechend der Verschiebung des Zustandes, weisen auch die Kreise bei gleicher Tunnelspannung unterschiedliche Radien auf.

Einfluss des Verzerrungsgitters auf den Grenzflächenzustand

Die Elektronen im Grenzflächenzustand sehen in unserem Fall auf der Salzinsel nicht nur die Stufenkanten und Adsorbate als Streuzentren, sondern nehmen auch das aus dem Wachstum resultierende Verzerrungsgitter als periodische Modulation des elektrostatischen Potentials wahr. Die hieraus resultierende Situation ist prinzipiell wohl bekannt aus den Grundlagen der Festkörperphysik: ein quasi-freies Elektronengas in einem schwachen periodischen Potential. Entsprechend dem Theorem von Bloch führt ein solches Potential zur Entstehung einer Bandlücke am Rand der Brillouin-Zone und einer Phasenverschiebung von π zwischen den Zuständen ober- und unterhalb der Bandlücke. Diese Bandlücke lässt sich in Fig. 5a bei einer Energie von ca. 0,27V als Dip im Spektrum der differentiellen Leitfähigkeit (näherungsweise die lokale Zustandsdichte an der Oberfläche) erkennen. Auch die Phasenverschiebung lässt sich bei unserem Probensystem durch Messung der differentiellen Leitfähigkeit nachweisen. Hierzu wurde eine Messserie aufgenommen, bei der ein und dieselbe Stelle der Probe bei verschiedenen Spannungen vermessen wurde. Hieraus kann im Anschluss eine Videosequenz erstellt werden, aus der deutlich hervorgeht, dass bei einer bestimmten Energie das Streifenmuster verschwindet, um bei nachfolgender Energieerhöhung mit der entgegengesetzten Phase wiederaufzutauchen.

Soweit sind unsere Beobachtungen noch gut vereinbar mit der fast 100 Jahre alten Theorie von Bloch. Anders als es die „Textbuchtheorie“ vorhersagt, bleibt die Periodizität des Verzerrungsgitters jedoch in unserem Experiment trotz Erhöhung der Energie konstant. Dies steht im krassen Widerspruch zur eigentlich parabolischen Dispersionsrelation des Grenzflächenzustands. Dies lässt sich besonders gut in der Fouriertransformation des Bildes erkennen. Während der Radius des Kreises entsprechend Dispersion mit ansteigender Tunnelspannung immer größer wird, bleiben die beiden zum Streifenmuster gehörenden Punkte konstant an einer Stelle, um nur während des Phasenwechsels kurz zu verschwinden. Es muss somit ein Mechanismus existieren, der es den Elektronenwellen ermöglicht in einer Dimension ihre Wellenlänge konstant zu halten, ohne die Energieerhaltung zu verletzen.

Links: Ein aus einer Bildserie von differentiellen Leitfähigkeitsmessungen erstelltes Video.

Rechts: Für jedes Bild der Messreihe wurde eine Fouriertransformation erstellt, wobei durch Wahl einer geeigneten Maske nur die Bereiche der NaCl-Insel in die Berechnung einfließen. Die Erhöhung der Tunnelspannung führt zu einer Verkleinerung der Wellenlänge der streuenden Elektronenwellen. Im reziproken Raum hat dies eine Vergrößerung des Radius zur Folge. Das Verzerrungsmuster bleibt sowohl im Ortsraum (Streifen behalten den gleichen Abstand) als auch im Wellenzahlraum (die 2 diskreten Punkte ändern ihre Position nicht) von der Energieänderung unbeeinflusst. Nur bei einer bestimmten Energie verschwindet das Verzerrungsmuster kurz, um im Folgenden mit einer Phasenverschiebung von π wieder zu erscheinen.