Ferroics

DFG Forschergruppe 1509 Ferroische Funktionsmaterialien
Mehrskalige Modellierung und experimentelle Charakterisierung
Funktionswerkstoffe sind seit dem Siegeszug der Elektronik fester Bestandteil quasi aller moderner technischer Geräte. Ihre Anwendungsgebiete erstrecken sich vom Automobil bis zur Raumfahrt, von Militäranwendungen bis hin zur Informations- und Kommunikationstechnologie. Sie tragen schon heute in hohem Maße zur Wertschöpfung bei. Eine Klasse dieser Werkstoffe sind die sogenannten „Smart Materials“. Diese sind in der Lage, eine physikalische Größe in eine andere zu transformieren. Hier sind als mögliche Umwandlungen beispielsweise Dehnungs- durch Temperaturänderungen, Magnetisierungsänderungen durch Dehnung, Viskositätsänderungen durch Magnetfelder, oder die Erzeugung mechanischer Spannungen aus elektrischen Feldern zu nennen. Je nach Anwendung kommen Skalen vom Nanometer bis hin zu Metern zum Tragen. Dementsprechend aufwendig ist eine umfassende Material- bzw. Bauteilcharakterisierung. Im Laufe der letzten Jahre ist eine vielzahl von Modellierungswerkzeugen entwickelt worden, die den Ingenieuren zunehmend erlauben, sehr kostspielige Experimente in großen Teilen der Entwicklung zu umgehen. In der Halbleiterindustrie beispielsweise ist der Wissensstand heute so weit fortgeschritten, dass ganze Rechnerarchitekturen aus dem Modell heraus entwickelt und gebaut werden können - praktisch ohne experimentelle Zwischenschritte. Aufgrund der komplexen Kopplungen zwischen den unterschiedlichen Feldgrößen ist solch ein Zugang für die Smart Materials derzeit noch nicht möglich. Einzelne Werkstoffeigenschaften sind in speziellen Modellen inzwischen hinreichend erfasst, aber die Vielfalt und wechselseitige Abhängigkeit der Effekte machen eine Modellierung, die das Bauteildesign aus der allgemeinen Werkstoffkenntnis heraus gestattet, derzeit noch unmöglich. Auch einige relativ simpel erscheinende Materialgesetze sind derzeit noch nicht in stabilen und robusten Algorithmen verankert.
Die Vision der Forschergruppe ist es, eine neue Qualität zuverlässiger, robuster Modellierungswerkzeuge für die Beschreibung der ausgeprägten Nichtlinearitäten und des komplexen Wechselspiels der unterschiedlichen Feldgrößen in ferroischen Funktionsmaterialien zu erreichen. Die erforderlichen experimentellen Daten werden sowohl originär im Rahmen eines Teilprojekts erstellt als auch aus zuverlässigen Literaturquellen entnommen. Da mögliche Ordnungsphänomene unterschiedlichster Natur sein können, wird sich die beantragte Forschergruppe auf die Kopplung von elektrischer Polarisation, Magnetisierung und Dehnung beschränken. Das Portfolio der geplanten Forschergruppe bilden somit ferroelektrische und ferromagnetische Werkstoffe sowie multiferroische Komposite. Die Eigenschaften von Funktionswerkstoffen bilden sich auf unterschiedlichsten Skalen heraus, einige bereits auf atomarer Ebene, z.B. die Magnetisierung, andere in der Einheitszelle eines Kristalls, wie die elektrische Polarisation, und andere erst, wenn diese jeweils über größere Längen oder Volumina miteinander koppeln und ordnen. Für technische Werkstoffe spielt hierbei oft das Gefüge eine entscheidende Rolle. Den Begriff Gefüge verwenden wir für die klassische Kornstruktur während die Mikrostruktur auch die funktionalen Domänenstrukturen mit einschließen soll.
Technologisch werden immer feinere Werkstoffe gefordert, die für die immer kleiner werdenden charakteristischen Längen der Bauteile geeignet sind. Als Beispiel sei der keramische Kondensator genannt, der ursprünglich aus Keramiklagen von ca.~50 µm Dicke aufgebaut war und heute nur noch 1 bis 2 µm dicke Lagen enthält. Die relevanten Korngrößen dürfen hierfür höchstens noch 100 nm betragen und sie werden immer kleiner. Dies führt dazu, dass auch die Mikrostruktur eine andere wird, da der Anteil der Korngrenzen stark steigt. Für magnetische Speicherchips liegt die charakteristische Längeneinheit bei 90 nm (Prototyp Infineon Stand 2007, neuester Industriestand 65 nm). Für Ferroelektrika werden Quantum-Dots inzwischen mit einer Größe von 60 nm im Labor hergestellt. Bei diesen Abmaßen wird das ganze System von Grenzflächen dominiert. Auch hier finden sich noch Domänensysteme und Ferroelektrizität, siehe Schilling et al..
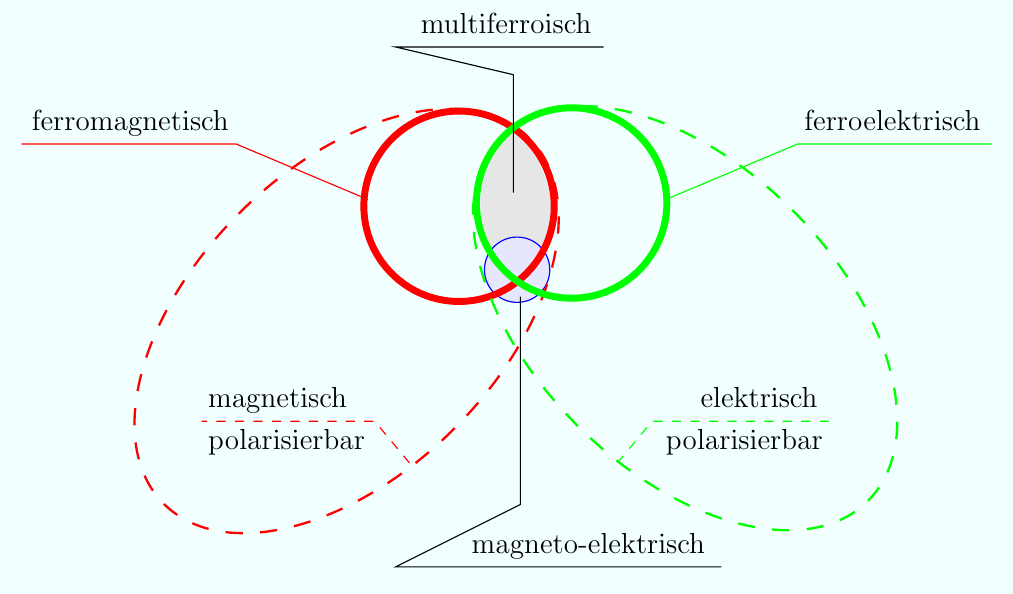
Entsprechend dieser technologischen Herauforderung soll die Forschergruppe auf mehreren Skalen tätig werden, von der Molekularstatik über die Mikrostrukturmodellierung bis hin zur phänomenologischen Bauteilbeschreibung mittels geeigneter Homogenisierungstechniken. Die Modellierung auf der jeweils kleineren Skala soll der nächst größeren als physikalische Basis und Motivation dienen, um so nicht rein empirische Modelle zu generieren. Unabhängig von der betrachteten Skala, gilt es, für alle Modelle die Stabilität und Robustheit der zugehörigen Algorithmen zu verbessern. Es gibt inzwischen eine Reihe von Modellen, die es z.B. gestatten, jeweils gewisse ferroelektrische Hysteresekurven nachzuvollziehen. Einige sind rein empirisch, andere nutzen einfache Homogenisierungstechniken. Fast alle leiden unter signifikanten Stabilitätsproblemen, insbesondere, wenn inhomogene Randbedingungen angelegt werden, wie z.B. bei vielachsiger Belastung. Praktisch kein Modellansatz existiert für die magneto -elektrisch koppelnden Komposite. Bei Raumtemperatur kommen nur Komposite als multiferroische Werkstoffe in Frage, da alle intrinsischen Multiferroika ihre Kopplungsphänomene und gemeinsamen Ordnungen nur bei sehr niedrigen Temperaturen ausbilden. Eine Ausnahme bildet das BiFeO3, das allerdings nur sehr kleine Kopplungsparameter aufweist. In der obenstehenden Abbildung werden die möglichen Kopplungen dargestellt. Unter den magneto-elektrischen Kopplungsmöglichkeiten gibt es solche ohne Remanenz (magnetisch oder elektrisch), komplett ferromagnetische und ferroelektrische, oder Mischformen (nach Eerenstein et al.). In Kompositen können je nach möglichem Herstellungsverfahren die jeweiligen Paarungen auch gezielt gewählt werden.
Ziele:
Die Forschergruppe hat sich zum Ziel gesetzt, eine neue Qualität im Bereich der
Beschreibung von komplexen, nichtlinearen, magneto-elektro-mechanischen
Interaktionen auf mehreren Skalen
zu erreichen, indem sie die Ergebnisse der folgenden Forschungsbereiche
zusammenführt:
- Modellierung der Evolution von Mikrostrukturen auf verschiedenen Skalen unter Verwendung atomistischer, phasenfeld- und relaxierungs-basierter Methoden sowie klassischer kontinuumsmechanischer Ansätze,
- Skalenübergänge und Homgenisierungstechniken für die Modellierung des effektiven Antwortverhaltens feldkoppelnder Materialien, sowie
- Messung einer repräsentativen, experimentellen Datenbasis des magneto-elektro-mechanischen Materialverhaltens zur Parameteridentifikation und Validierung.
Die Ergebnisse bieten eine umfassende Grundlage für den simulationsbasierten Entwurf von neuen Materialien und „High-Tech“-Bauteilen mit multifunktionellen Eigenschaften.
Diese Ziele sind nur durch die Bündelung von Kompetenzen aus dem Bereich der Kontinuumsthermodynamik, der computerorientierten Mechanik und der Materialwissenschaft zu erreichen. Deshalb ist die Forschergruppe aus Experten dieser Bereiche zusammengesetzt. Nur gemeinsam können sie die Herausforderungen bewältigen, die sich bei der Beschreibung und Charakterisierung der magnetisch, elektrisch und mechanisch koppelnden Materialien ergeben.
Literatur
W. Eerenstein, M. Wiora, J. Prieto, J. F. Scott and N. Mathur (2007), "Giant sharp and persistent converse magnetoelectric effects in multiferroic epitaxial heterostructures", Nature Materials, May, 2007. Vol. 6(5), pp. 348-351.
A. Schilling, D. Byrne, G. Catalan, K. G. Webber, Y. A. Genenko, S. G. Wu , J. F. Scott and J. M. Gregg (2009), "Domains in Ferroelectric Nanodots", Nano Letters., September, 2009. Vol. 9(9), pp. 3359-3364.
