Bearbeiter: Dipl.-Ing. A. Kisse , PD Dr.-Ing. K. Lesny, Dr. Ing. A. Kisse (seit Mai 2008 CDM Consult GmbH, Bochum)

Förderung durch: DFG

Kurzbeschreibung des Projekts:

Die Kenntnis der Wechselwirkungen zwischen Bauteil und Boden ist entscheidend für eine sichere, aber zugleich wirtschaftliche Bemessung. Geotechnische Nachweiskonzepte unterscheiden hierbei im allgemeinen zwei Grenzzustände, den Grenzzustand der Tragfähigkeit und den Grenzzustand der Gebrauchstauglichkeit.
So ist z. B. für eine Flachgründung nachzuweisen, dass Versagen des Baugrunds mit einer definierten Sicherheit ausgeschlossen werden kann und die zu erwartenden Setzungen verträglich sind. Die Ansätze zur Beschreibung dieser Grenzzustände sind nicht konsistent, da sie unterschiedliche Bodeneigenschaften voraussetzen. So beruht die Setzungsermittlung auf der Annahme linear-elastischen Materialverhaltens. Bei Ermittlung des Bruchzustands wird hingegen ideal-plastisches Materialverhalten angenommen, wobei nochmals verschiedene Grenzzustände unterschieden werden.

Ein Systemgesetz, welches eine konsistente Beschreibung des Systemverhaltens unter äußerer Belastung bis zum Versagen der Gründung beschreibt, macht eine solche Unterscheidung in verschiedene Grenzzustände überflüssig.

Das Systemgesetz besteht hierbei aus einer Verschiebungsregel, die die Beziehung zwischen äußerer Belastung und Verschiebung bzw. Verdrehung des Fundaments beschreibt, und einer Versagensbedingung, die die Grenztragfähigkeit der Gründung in Abhängigkeit von der äußeren Belastung definiert. Die Versagensbedingung stellt zudem eine notwendige Nebenbedingung für die Verschiebungsregel dar, da der Zuwachs der Verschiebungen abhängig ist von der Größe der vorhandenen Last im Vergleich zur Bruchlast. Weiterhin erfordert die Herleitung der Verschiebungsregel die konsistente Formulierung der Grenztragfähigkeit ohne die bisherige Aufspaltung in einzelne Grenzzustände (Grundbruch, Gleiten, Kippen, Auftrieb). Ein Ansatz, der die Anforderung erfüllt, beruht auf der Darstellung der Grenztragfähigkeit im Raum der äußeren Lasten und wird als Interaktionsansatz bezeichnet (Lesny, 2001).

Die Herleitung des Systemgesetzes gliedert sich damit in zwei Schritte:

1. Definition der Versagensbedingung

Die Versagensbedingung stellt eine notwendige Nebenbedingung für die Verschiebungsregel dar, da der Zuwachs der Verschiebungen abhängig ist von der Größe der vorhandenen Last im Vergleich zur Bruchlast. Die spätere Herleitung der Verschiebungsregel erfordert die konsistente Formulierung der Grenztragfähigkeit ohne die bisherige Aufspaltung in einzelne Grenzzustände. Ein Ansatz, der diese Anforderung erfüllt, beruht auf der Darstellung der Grenztragfähigkeit im Raum der äußeren Lasten und wird als Interaktionsansatz bezeichnet. Dadurch kann der aus den einzelnen Nachweisen resultierende zulässige Belastungsbereich unmittelbar beschrieben werden.

Für Fundamente ohne Einbindetiefe auf nichtbindigem Boden konnte der Interaktionsansatz für den allgemeinen Belastungsfall formuliert und seine Parameter anhand von Versuchsergebnissen verifiziert werden. Für Fundamente mit Einbindetiefe bzw. auf bindigem Boden ist es gelungen, die Grundform des Ansatzes zu erweitern. Die die Lastinteraktionen beeinflussenden Systemgrößen konnten identifiziert und die Parameter hinsichtlich ihrer Größenordnung abgeschätzt werden (Lesny, 2001).

2. Definition der Verschiebungsregel

Die Verschiebungsregel beschreibt den Last-Verschiebungsverlauf bis zum Erreichen des Versagenszustands. Aufgrund der im allgemeinen räumlichen Fall sehr komplexen Belastungssituation kommt zur Formulierung der Verschiebungsregel nur ein tensorieller Ansatz infrage. Der mathematische Ansatz zur Beschreibung des Last-Verformungsverhaltens lautet dementsprechend allgemein . Hierin ist der dimensionslose Belastungsvektor mit den Komponenten Vertikallast, Horizontallasten, Torsionsmoment und Biegemomente und der dazu korrespondierende dimensionslose Verformungsvektor mit den Verschiebungen und Verdrehungen des Systems.

u = K * Q

Hierin ist Q der Belastungsvektor mit den Komponenten Vertikallast, Horizontallasten, Torsionsmoment und Biegemomente und u der dazu korrespondierende Verformungsvektor mit den Verschiebungen und Verdrehungen des Systems. Der Tensor K stellt somit eine Beziehung zwischen den Belastungen und den dazu korrespondierenden Verformungen dar (Kisse, 2002). Eine mathematische Formulierung des Tensors K erfolgt hierbei auf den Prinzipien der isotropen Verfestigung der Plastizitätstheorie.

Zudem sind diese Last-Verschiebungsverläufe in den meisten Fällen nichtlinear. Nur weit unterhalb der Bruchlast sind sie näherungsweise linear. Des Weiteren ist das Systemverhalten unter vielfältiger Belastung sehr komplex, so treten Verschiebungs- bzw. Verdrehungskomponenten nicht allein in Richtung der korrespondierenden Belastung auf, wie die unten stehende Abbildung zeigt.

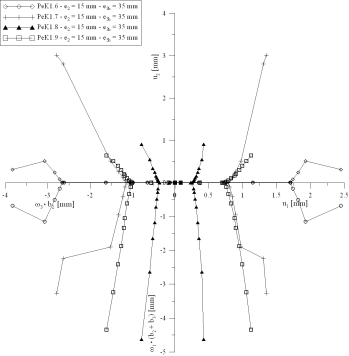
Abb.: Verschiebungen und Verdrehungen eines Modellfundamentes unter komplexer Belastung

Die bisherigen Untersuchungen basieren hauptsächlich auf der Auswertung kleinmaßstäblicher Modellversuche sowie weniger Großversuche. Trotz der Vielzahl verfügbarer Versuchsergebnisse wird das im Rahmen der oben beschriebenen Aufgabe zu untersuchende Lastspektrum bei weitem nicht abgedeckt. Dies betrifft insbesondere Kombinationen aus mehr als zwei Lastkomponenten.

Neben der physikalischen Modellierung besteht grundsätzlich die Möglichkeit, die Interaktion Fundament-Boden unter äußerer Last mit Hilfe numerischer Berechnungen auf Basis der FEM zu simulieren. Dies ist gerade für die Analyse der Fundamentverschiebungen bzw. -verdrehungen unter komplexer äußerer Belastung interessant, weil der zu untersuchende Belastungsbereich einschließlich verschiedener Lastpfade sowie Be- und Entlastungsphasen durch physikalische Modellierung kaum abzudecken ist.

 Dreidimensionale Berechnungen, wie sie für den hier zu untersuchenden Fall eines Einzelfundaments notwendig sind, sind in der Literatur jedoch nur selten zu finden. Bekannt ist z. B. die Nachrechnung eines Feldversuchs mit einem Einzelfundament unter schräg-ausmittiger Belastung (Williams et Hicks, 1992; Hügel, 1995; von Wolffersdorff, 1997). Aus diesem Grund soll innerhalb dieses Projekts umfassend geprüft werden, ob und auf welche Weise die Wechselwirkungen zwischen kombinierter, äußerer Belastung und korrespondierenden Verschiebungen bzw. Verdrehungen eines Einzelfundaments zuverlässig numerisch simuliert werden können. Die Berechnungen werden mit dem Programmsystem ABAQUS (2000) durchgeführt, das dreidimensionale Modellierung ermöglicht und gerade in der Geotechnik sehr häufig verwendet wird.

Abb.: ABAQUS-Plot

Für die Anwendung probabilistischer Methoden, die zunehmend bei Risikoanalysen oder Wirtschaftlichkeitsbetrachtungen komplex belasteter Systeme eingesetzt werden, ist die geschilderte Nachweisstruktur besser geeignet als die zur Zeit gültigen Verfahren. Bei denen bedeutet das Versagen eines Systems den Verlust seiner Funktionsfähigkeit und umfasst damit zwangsläufig die Grenztragfähigkeit und die Gebrauchsfähigkeit. Bei Unterscheidung verschiedener Grenzzustände kann die Wahrscheinlichkeit des Verlusts der angestrebten Funktion somit nur abgeschätzt werden. Sie ist wegen der vielfachen Korrelationen der Nachweise nicht exakt bestimmbar. Derartige Untersuchungsverfahren erfordern daher die Beschreibung des Systemverhaltens unter äußerer Belastung durch ein Modell, auf dessen Grundlage die Versagenswahrscheinlichkeit bestimmt werden kann.

Veröffentlichungen

Kisse, A.; Lesny, K. (2005):
Single surface hardening model - a system law to describe the foundation-soil interaction. In: Proc. of the Int. Symposium on Frontiers in Offshore Geotechnics (ISFOG 2005), Perth, Australien, S. 483-489

Lesny, K.; Kisse, A. (2004):
Safety of Shallow Foundations in Limit State Design. In: Proc. of the Int. Workshop on Risk Assessment in Site Characterization and Geotechnical Design, Bangalore, Indien, S. 97-109

Kisse, A. (2003):
Entwicklung einer Verschiebungsregel zur Beschreibung der Verschiebungen von Fundamenten auf Sand. In: 27. Baugrundtagung Mainz, Spezialsitzung "Forum für junge Geotechnik-Ingenieure", Mainz 2002, S. 14-15

Lesny, K.; Kisse, A; Richwien, W. (2003):
Proof of Foundation Stabililty Using a Consistent Failure Model. In: Proceedings of the International Conf. on Probabilistics in Geotechnics -Technical and Economic Risk Estimation, Graz, Austria, S. 95-103

Lesny,K.; Richwien, W. (2002):
A Consistent Failure Model for Single Footings embedded in Sand. In: Proceedings of the International Workshop on Foundation Design Codes and Soil Investigation in View of International Harmonization and Performance Based Desing, IWS Kamakura, Tokyo, Japan, S. 159-165

Lesny,K. (2002):
Zum Nachweis der Standsicherheit von Fundamenten auf Basis eines konsistenten Versagensmodells. In: Bautechnik 79, Heft 2, S. 78-83

Kisse, A. (2001):
A consistent description of the serviceability and ultimate limit states of foundations. In: Proceedings of the XIV. Young Geotechnical Engineers Conference, Plovdiv, Bulgaria

Lesny, K. (2001):
Entwicklung eines konsistenten Versagensmodells zum Nachweis der Standsicherheit flachgegründeter Fundamente. Essen: Glückauf-Verlag, 2001 (Mitteilungen aus dem Fachgebiet Grundbau und Bodenmechanik, Heft 27, Hrsg. W. Richwien)

Lesny, K. (2000):
Nachweis der Standsicherheit von Fundamenten mit Interaktionsansätzen. In: 26. Baugrundtagung Hannover, Spezialsitzung "Forum für junge Geotechnik-Ingenieure", Hannover 2000, S. 63

Golücke, K. (1998):
Entwicklung eines konsistenten Versagensmodells zur Berechnung der Standsicherheit von Flachgründungen. In: 25. Baugrundtagung Stuttgart, Spezialsitzung "Forum für junge Geotechnik Ingenieure", Stuttgart 1998, S. 14

Perau, E. (1998):
Ein konsistentes Versagensmodell zum Standsicherheitsnachweis flachgegründeter Fundamente. In: Beiträge zur aktuellen Forschung in Grundbau und Bodenmechanik, Essen: Glückauf-Verlag, 1998 (Mitteilungen aus dem Fachgebiet Grundbau und Bodenmechanik, Heft 23, Hrsg. W. Richwien), S. 95-103

Perau, E. (1997):
Design of Shallow Foundations Using Interaction Diagrams. In: Proceedings of the XIV. International Conference On Soil Mechanics and Foundation Engineering, Hamburg, Vol. 2, pp. 1193-1196, Balkema, Rotterdam

Weitere Informationen

Beim 8. Essener Geotechnik Kolloquium (27.04.2004) wurde das Systemgesetz vorgestellt. Die Folien des Vortrages können hier heruntergeladen werden (pdf-Dokument, ca. 320 kB):

Systemgesetz als konsistente Berechnungsmethode für Flachfundamente

Im Rahmen des Int. Symposium on Frontiers in Offshore Geotechnics (ISFOG 2005) in Perth wurde das Systemgesetz auch anhand eines Posters erläutert (pdf-Dokument, ca. 820 kB).