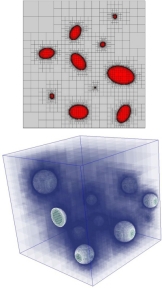
Automatic mesh generation and analysis

We are developing efficient mesh generation and analysis algorithms which can be used to investigate elastostatic and elastodynamic processes in solids with highly irregular geometrical properties. The scaled boundary finite element method (SBFEM) is employed – a semi-analytical technique which can be used for the simulation of static and dynamic phenomena in highly heterogeneous two- and three-dimensional domains on structured, incompatible meshes. The automatic generation of quadtree and octree meshes from digital images and CAD data is the subject of current research. Special algorithms are developed to create appropriate meshes for wave propagation in geological structures based on the frequency content and material data. The proposed methods can be used in the context of numerical homogenization and uncertainty quantification of effective properties of solids with random microstructure characteristics.

These research activities are associated with the core research area „Tailored Materials“ of the Faculty of Engineering and with the strategic programme „Materials Chain“ of the University Alliance Ruhr.

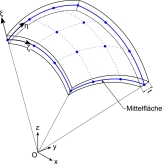
Semi-analytical plate and shell elements

The development of locking-free elements for thin-walled structures is the subject of current research. In particular, shell elements are derived based on the scaled boundary finite element method (SBFEM). Using this semi-analytical approach, a discrete formulation of the linear elastostatic problem in the circumferential directions is combined with an analytical solution in the radial direction. We expect to minimize locking effects due to the exact description of the through-thickness behaviour. Current research focusses on method development as well as on convergence studies and locking phenomena.

Advanced discretization techniques

Classical discretization methods – such as the finite element method and the finite difference method – are progressively being enhanced or even replaced by novel concepts. In our research, we are investigating and further developing such advanced discretization techniques. In particular, the formulation of general polygonal and polyhedral elements has been proven to be a promising and rapidly evolving approach due to their highly flexible geometry approximation compared to conventional triangular and quadrilateral finite elements. Interpolations over polygonal and polyhedral domains can be derived based on the semi-analytical scaled boundary finite element method (SBFEM). Furthermore, approaches based on high-order polynomial interpolation are addressed. Within the framework of polygonal elements, so-called quadtree- and octree-discretizations form an interesting special case. Such meshes consist of square-shaped or cubic cells only and are ideally suited to discretize image-based datasets. Likewise based on the SBFEM, we are developing semi-analytical prismatic elements, which require only the discretization of a structure’s cross-section. Apart from the mentioned semi-analytical methods, we are exploring different advanced discretization techniques such as isogeometric analysis and the finite cell method.

Simulation of wave propagation phenomena

One of the key subjects of this institute is the investigation of various wave propagation phenomena by means of numerical and (semi-)analytical methods. The main focus is on elastic as well as acoustic waves in structures relevant for engineering science and applications. We are creating new approaches and algorithms to model complex problems more efficiently by employing and further developing a wide range of concepts. Particularly, we are concerned with finite and spectral elements, semi-analytical techniques, polygonal elements, image-based mesh generation and isogeometric analysis. For instance, in recent projects we are assessing the propagation of elastic waves through layered media of complex geometry and the behavior of guided ultrasonic waves for applications in non-destructive testing and material characterization.