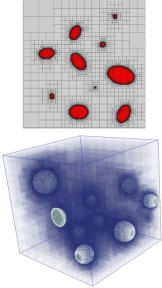
Automatische Netzgenerierung und Berechnung

Im Fachgebiet Statik und Dynamik der Flächentragwerke werden effiziente Vernetzungs- und Berechnungsalgorithmen entwickelt, die sich für die Untersuchung elastostatischer und elastodynamischer Vorgänge in Festkörpern mit ungleichmäßigen geometrischen Eigenschaften eignen. Zum Einsatz kommt die „Scaled Boundary Finite Element Method“ (SBFEM). Diese semi-analytische Methode erlaubt die Verwendung von inkompatiblen, strukturierten Netzen für die Simulation statischer und dynamischer Prozesse auf stark heterogenen zwei- und dreidimensionalen Gebieten. Gegenstand der aktuellen Forschung ist die automatische Erzeugung von Quadtree- und Octree-Netzen aus digitalen Bilddaten und CAD-Daten. Zur Modellierung von Wellenausbreitungsvorgängen in geologischen Strukturen werden spezielle Algorithmen unter Berücksichtigung des Frequenzgehaltes entwickelt. Weitere potentielle Anwendungsgebiete der entwickelten Methoden sind die Berechnung effektiver Materialkenngrößen im Zusammenhang mit numerischer Homogenisierung sowie die Unschärfequantifizierung der Eigenschaften von Materialien mit zufällig verteilter Mikrostruktur.

Unsere Arbeiten auf diesem Gebiet sind den Forschungsschwerpunkten „Tailored Materials“ der Fakultät Ingenieurwissenschaften und „Materials Chain“ der Universitätsallianz Ruhr zugeordnet.

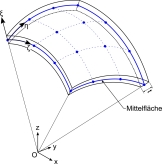
Semi-analytische Elemente für Platten und Schalen

Die Entwicklung von versteifungsarmen Elemente zur Flächentragwerksmodellierung ist Gegenstand dieses Forschungsschwerpunkts. Abgeleitet werden Schalenelemente auf der Grundlage der „Scaled Boundary Finite Element Method“ (SBFEM). Da diese semi-analytische Methode auf der Kombination einer diskreten Darstellung in Umfangsrichtung mit einer semi-analytischen Lösung in radialer Richtung beruht, wird erwartet, dass Locking-Effekte vermieden werden. Aktuelle Forschungsbemühungen widmen sich der Methodenentwicklung sowie der Untersuchung von Konvergenz- und Versteifungseigenschaften.

Nichtklassische Diskretisierungsverfahren

Klassische diskretisierende Verfahren - wie die Finite Elemente Methode oder die Finite Differenzen Methode – werden zunehmend durch neue Konzepte erweitert oder gar ersetzt. In diesem Fachgebiet werden verschiedene dieser Ansätze untersucht und weiterentwickelt. Besonders umfassend und vielversprechend ist die Formulierung allgemeiner polygonaler Elemente, die eine wesentlich flexiblere Geometriebeschreibung erlauben als herkömmliche drei- und vierseitige Finite Elemente. Solche polygonalen Elemente können insbesondere auf Basis der Scaled Boundary Finite Element Method (SBFEM) formuliert werden. Zudem werden Ansätze auf Grundlage polynomischer Interpolation hoher Ordnung entwickelt. Ein Sonderfall polygonaler Elemente stellen Quadtree- und Octree-Diskretisierungen dar, die ausschließlich aus Elementen quadratischer bzw. kubischer Form bestehen und sich zur effizienten Diskretisierung bildbasierter Datensätze eignen.

Ebenfalls basierend auf der SBFEM werden prismatische Elemente entwickelt, die nur eine Diskretisierung des Querschnittes einer Struktur konstanter Dicke erfordern. Neben diesen überwiegend semi-analytischen Ansätzen zählen zu den nichtklassischen Diskretisierungsverfahren beispielsweise die isogeometrische Analyse sowie die Finite Cell Method.

Simulation von Wellenausbreitungsphänomenen

Ein Forschungsschwerpunkt des Fachgebietes besteht in der Untersuchung verschiedener Wellenausbreitungsphänomene mit Hilfe numerischer und (semi-)analytischer Modelle. Im Fokus liegen elastische und akustische Wellen in Strukturen von praktischer Relevanz für ingenieurwissenschaftliche Fragestellungen. Es werden neue Ansätze und Algorithmen zur effizienten Simulation komplexer Probleme entwickelt. Zu diesem Zweck werden aktuelle Konzepte der Simulation und Modellierung kombiniert und weiterentwickelt. Zum Einsatz kommen insbesondere spektrale Elemente, semi-analytische Verfahren, polygonale Elemente, bildbasierte Netzgenerierung und isogeometrische Analyse. In aktuellen Projekten untersuchen wir beispielsweise das Verhalten elastischer Wellen in geschichteten Strukturen komplexer Geometrie sowie die Ausbreitung geführter Ultraschallwellen für die Anwendung in zerstörungsfreier Schadensdetektion und Materialcharakterisierung.