Sommer 2018

Dezember 2017

3 aus 12!
Aus den zwölf Punkten des abgebildeten Gitters werden zufällig drei ausgewählt. ​Wie groß ist die Wahrscheinlichkeit, dass diese drei Punkte auf einer Geraden liegen?

​

 

November 2017: Im "Haus der Vierecke"

​In einem Quadrat wird ein beliebiger Punkt I im Inneren mit den Ecken verbunden und die entstehenden Dreiecke werden abwechselnd grau und weiß gefärbt.

​
​

​

​​

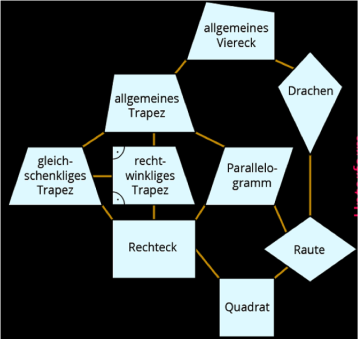
Beweisen Sie: für jeden inneren Punkt I ist die Summe der Flächeninhalte der grauen Dreiecke gleich der Summe der Flächeninhalte der weißen Dreiecke. Gibt es noch andere Vierecke (außer dem Quadrat), für die dies auch gilt? Wenn ja, welche? Für welche Vierecke gilt dies nicht für jeden inneren Punkt I? Für welche Punkte I gilt es dann trotzdem? Wie weit kommen Sie im „Haus der Vierecke“?

Hinweis: zum Experimentieren können Sie sich gerne die GeoGebra-Datei „flaechen.ggb“ auf der PdM-Webseite herunter­laden: Flächen
Vergessen Sie aber nicht das Beweisen ihrer Befunde.

Oktober 2017: Ohne Karte ins Kino!
In der Lobby eines Kinos warten 111 Gäste darauf, in den Vorführungssaal gelassen zu werden. In diesen passen exakt 111 Personen – die Vorstellung ist also ausverkauft!
​

​​Der Einlass beginnt! Die 111 Gäste stellen sich in einer Schlange auf. Die Frau, die ganz vorn steht, hat jedoch ihre Karte verloren. Der Kartenabreißer glaubt ihr und lässt sie glücklicherweise auch ohne Karte in den Saal. In dem Kino gibt es keine freie Platzwahl. Da die Dame ihren Sitzplatz nun nicht mehr ablesen kann, setzt sie sich einfach auf einen zufällig ausgewählten Platz. Alle folgenden Gäste setzen sich auf den Sessel, der auf ihrem Ticket steht. Sollte dieser Platz jedoch belegt sein, suchen sie sich wie die Dame vorn in der Schlange einen noch freien Platz aus.

Frage: Wie hoch ist die Wahrscheinlichkeit, dass die Person an letzter Stelle der Schlange, also Kinogast Nummer 111, es sich auf dem Sessel gemütlich machen kann, der auch auf seiner Einlasskarte steht?

 

Juli 2017
Die kaputte Uhr: Meine Uhr ist stehengeblieben. Der kleine Zeiger zeigt ungefähr auf 10 und der große Zeiger ungefähr auf 2. Beide Zeiger bilden einen identischen Winkel zur 12.
​

Wann ist die Uhr genau (sekundengenau) stehengeblieben?

Erläutern Sie Ihre Lösungsstrategie!

 

Juni 2017
Es wird so lange eine Münze geworfen, bis das erste mal „Kopf“ fällt. Zeigt die Münze beim ersten Wurf „Kopf“, beträgt die Auszahlung 2 Euro. Zeigt die Münze beim zweiten Wurf „Kopf“, so verdoppelt sich die Auszahlung auf 4 Euro, zeigt sich „Kopf“ hingegen erst beim dritten Wurf, sind es schon 8 Euro – usw. Bis zu welchem Wetteinsatz sollte ein Spieler dieses Spiel noch akzeptieren?

Mai 2017
Wie können sieben Bäume so gepflanzt werden, dass es sechs gerade Baumreihen mit je drei Bäumen gibt? Wie sieht es mit zehn Bäumen, fünf Reihen zu je vier Bäumen aus?

April 2017
Sechs Osterhasen haben sich jeweils ein sensationelles neues Rezept für Schokoladeneier ausgedacht. Um die Rezepte auszutauschen, telefonieren die Osterhasen miteinander. Dabei gibt jeder Osterhase alle Rezepte weiter, die ihm derzeit bekannt sind. Wie viele Telefonate sind nötig, damit am Ende jeder Osterhase alle sechs Rezepte kennt? Begründen Sie. Weitergedacht: Wie sieht das für sieben oder acht Hasen aus? Frohe Ostertage!

 

 

 

 

März 2017

Sie kennen vielleicht das „mathematische Spiel“ immer drei mal drei. Es geht dabei darum, mit genau drei 3en möglichst viele verschiedene Zahlen darzustellen. Erlaubt ist dabei fast alles, was man mit Zahlen machen kann. Rechenzeichen, Klammern und Kommata einfügen, Wurzeln ziehen und vieles mehr. Zum Beispiel:

​

​
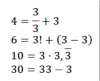
Wir spielen nun eine Variante dieses Spiels mit den Ziffern 1, 2, 3, 4 und 5. Jede dieser fünf Ziffern soll dabei genau einmal vorkommen, z.B. 7=(15−4+3):2
Aufgabenteil a) Finden Sie eine Darstellung für alle Zahlen von 1 bis 40 mithilfe der Ziffern 1 bis 5 unter den oben genannten Regeln.
Aufgabenteil b) Welche Zahlen waren besonders schwierig darzustellen? Können Sie Gründe dafür angeben, dass bestimmte Zahlen schwieriger als andere darzustellen sind?
Aufgabenteil c) Finden Sie möglichst viele verschiedene Darstellungen für die Zahl 42.

 

Januar 2017

Kryptogramme sind Aufgaben, in denen Symbole oder Buchstaben für Ziffern oder Zahlen stehen. Beim Entschlüsseln dieser Aufgabe kommt es darauf an, die Buchstaben so zu ersetzen, dass richtig gelöste Aufgaben entstehen. Hier stehen gleiche Buchstaben für gleiche Ziffern, verschiedene Buchstaben stehen für verschiedene Ziffern. Lösen Sie folgende Aufgabe:

   V I E R
+ E I N S
—————
F U E N F

Geben Sie alle Lösungen an. Stellen Sie Ihr Vorgehen ausführlich und begründet dar

Dezember 2016

Max (M) geht mit seinem Hund Tommy im Wald spazieren. Plötzlich taucht unerwartet ein Schneesturm auf und nach kurzer Zeit sieht die Umgebung ganz anders aus. Max ist verwirrt und macht sich Sorgen, wie er denn jetzt wieder zur Straße kommt. Er weiß, dass er sich 1 km vom Rand eines riesigen Waldgebietes befindet, hat aber keine Ahnung in welcher Richtung der Rand liegt. Die Straße, welche eine Gerade ist, liegt genau am Rande des Waldgebietes. Auch Tommy ist völlig desorientiert, da der Schnee alle Spuren beseitigt hat. Beide wissen nicht in welche Richtung sie gehen müssen, um den Rand und somit den Ausgang des Waldes bzw. die Straße zu finden. Gibt es unter den gegebenen Voraussetzungen eine Strategie, das Waldgebiet zu verlassen und die Straße zwingend zu erreichen? Wie sollte sich Max mathematisch optimal verhalten?

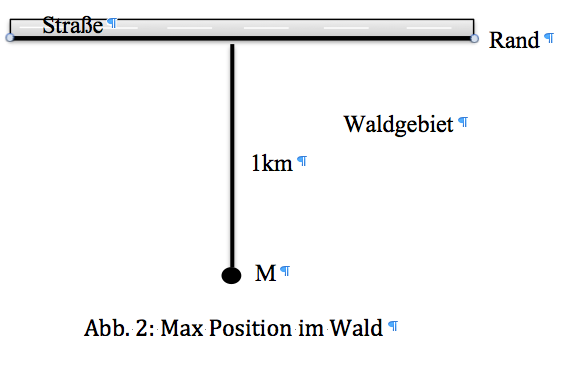
November 2016

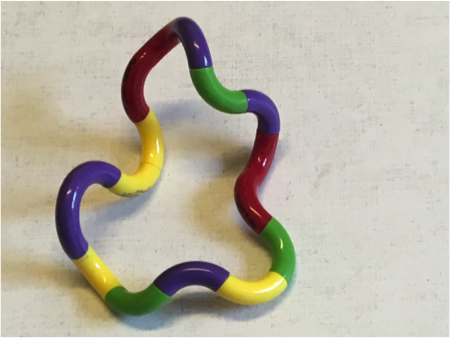
Aus den abgebildeten Elementen sollen geschlossene, zusammenhängende Gebilde geschaffen werden, indem die Teile - wie in den Beispielen unten - einfach zusammen gesteckt werden. Bei welchen Anzahlen von Elementen kann man das zusammengebaute Gebilde flach auf den Tisch legen (s. Beispiel rechts)? Begründen Sie Ihre Antwort gründlich.
Wenn Sie Lust haben, denken Sie weiter: Wie verändert sich die Antwort, wenn man Halbkreise, Drittelkreise, Fünftelkreise, ... verwendet?

Oktober 2016:
Gegeben sei ein Kreissektor OAB mit r = 1.

Diesem Kreissektor werden vom Kreisbogen AB aus sich berührende Kreise einbe­schrieben, so dass sich eine unendliche Reihe stetig kleiner werdender Kreise ergibt. In der Abb. sind nur die ersten drei dieser Kreise eingezeichnet.

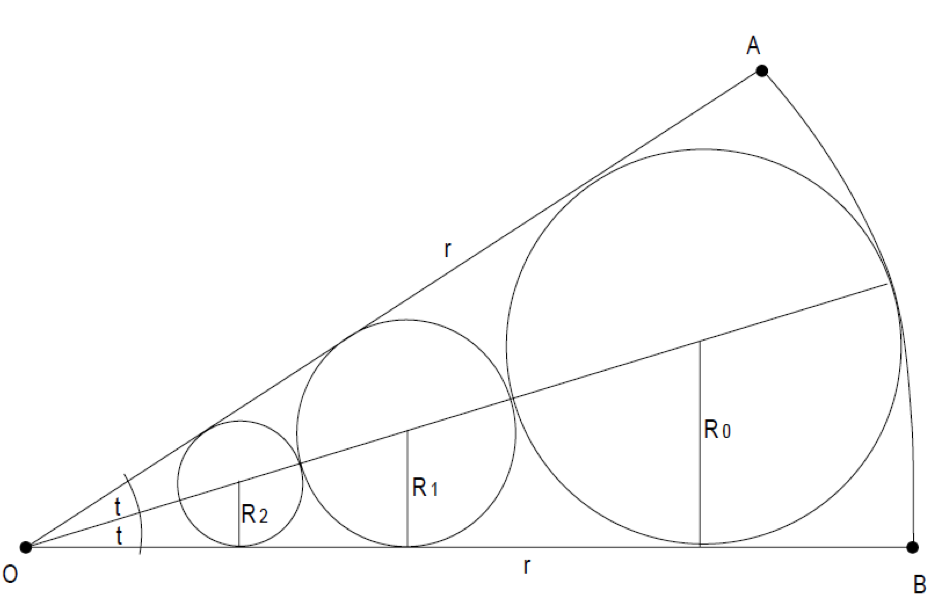
Bei welchen Mittelpunktswinkel 2t des Kreissektors wird der Anteil der Summe aller Kreis­flächen­inhalte am Kreissektor maximal? (bei welchem Winkel ist also das Verhältnis aus Kreisflächensumme und Kreissektor­fläche am größten?)

Welcher Prozentsatz des Kreissektors wird dann von den Kreisflächen über­deckt?

 

Juli 2016:

Von einem Quader sind die Kantenlängen bekannt: a = 10 cm, b = 6 cm, c = 4 cm

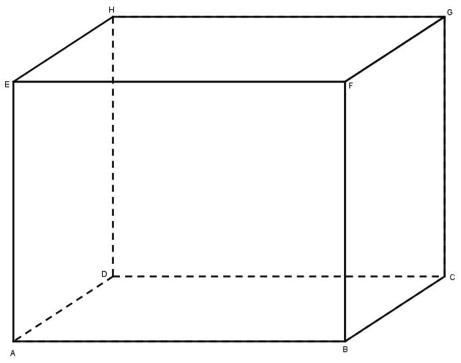Gesucht ist ein Quader, dessen Oberfläche halb so groß ist. Finden Sie alle Quader mit ganzzahligen Kantenlängen, für die das gilt.

 

 

Juni 2016:

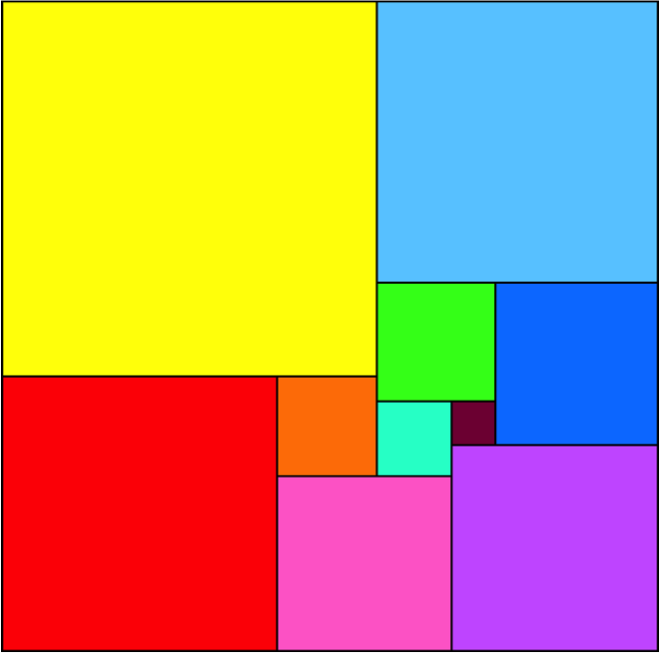
Wie große sind die einzelnen Quadrate mindestens, wenn sie alle verschieden groß und ganzzahlig sind? Erläutern Sie ihre Lösungsstrategie!

Mai 2016:

Wie viel Liter Benzin kann ein Paketdienstleister in Deutschland bei der Auslieferung der Pakete sparen, wenn die Fahrer auf ihren Routen größtenteils rechts abbiegen anstatt links? Stellen Sie ausführlich dar, wie Sie zu Ihrer Antwort gekommen sind und welche Annahmen Sie zur Modellierung des Problems getroffen haben!

 

 

März 2016:

Uni solar?
Extra zum Frühlingsanfang stellen wir Ihnen die Frage:

"Könnte sich unsere Universität autark mit Strom durch Sonnenenergie versorgen?".

Bitte berücksichtigung Sie bei der Lösung der Fragestellung auch den Platzbedarf für eine Solaranlage, ihre durchschnittliche Lebensdauer, die Wartungskosten, die Finanzierung über Kredite, eine staatliche Förderung etc.

Stellen Sie ausführlich dar, wie sie zu Ihrer Antwort gekommen sind und welche Annahmen Sie zur Modellierung des Problems getroffen haben!
 

Februar 2016: Wie groß ist die Ringfläche?

 

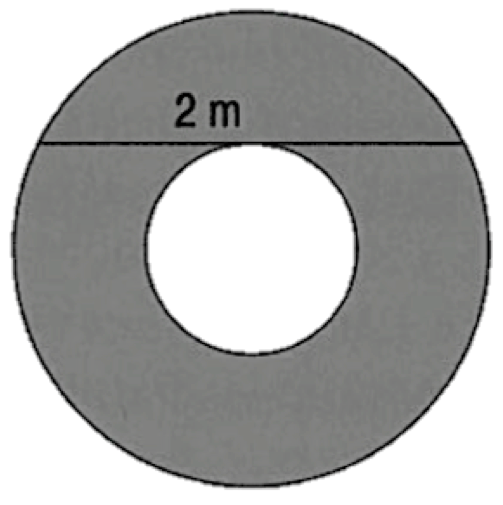
Januar 2016:

Gibt es ein natürliche zehnstellige Zahl, für die folgende Bedingungen gelten: 

1. Jede Ziffer (0, 1, …, 9) darf genau einmal vorkommen.
2. Die ersten n Stellen der Zahl sind durch n teilbar.

Gibt es darüber hinaus noch weitere Zahlen, die beide Bedingungen erfüllen? Beweisen Sie! Beispiel: Die dreistellige Zahl 123 würde die gegebenen Bedingungen erfüllen.

1. Jede Ziffer kommt genau einmal vor.
2. die ersten n Stellen der Zahl sind durch n teilbar

• die erste Stelle (1) ist durch 1 teilbar,
• die ersten zwei (12) Stellen sind durch 2 teilbar,
• die ersten drei Stellen (123) sind durch 3 teilbar.

Dezember 2015: Erbsen schätzen
Schätzen Sie, wie viele getrocknete Erbsen in dieser Vase sind!
Stellen Sie ausführlich dar, wie Sie zu Ihrer Schätzung kommen. Geben Sie dabei an, welche Annahmen Ihren verschiedenen Abschätzungen zugrunde liegen und erläutern Sie Ihre Rechnung nachvollziehbar.

Information:

• die Vase hat eine annähernd elliptische Grundfläche
• die lange Achse hat eine Länge von 17 cm

----------------------------------------------------------------------------------------------------------------------------------------
November 2015:
Welche der Zahlen 1, 11, 111, 1111, 11111, 111111, ... sind durch 29 teilbar?
----------------------------------------------------------------------------------------------------------------------------------------
Oktober 2015: Zusammenfassung schreiben
Zwei Studierende, Johann und Sascha, schreiben dieselbe Klausur und wollen sich gemeinsam darauf vorbereiten. Wie schon oft geschehen, beschließen sie, sich die Arbeit bei der Zusammenfassung zu teilen. Aus Erfahrung und anhand der Gesamtzahl der Seiten im Skript wissen sie, dass Johanna, sollte sie die Zusammenfassung alleine erstellen - 15 Stunden länger als Sascha benötigen würde. Zusammen benötigen sie 56 Stunden.
Frage:
Wie lange würden die beiden jeweils am Schreibtisch sitzen, wenn jeder eine eigene Zusammenfassung erstellen würde? Begründen Sie!
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
September 2015: Gameshow
In der Gameshow „Alles oder nichts“ gibt es momentan den beachtlichen Jackpot von zehn Millionen Euro zu gewinnen. Dementsprechend groß waren der Andrang der Bewerber und die Konkurrenz innerhalb der Gruppen, die nach einer Vorauswahl schließlich in der Liveshow teilnehmen konnten. Im Finale steht nun die stärkste, kreativste, klügste und cleverste Gruppe und wie der Titel der Show schon vermuten lässt, geht es für sie jetzt um „alles oder nichts“.

Um die zehn Millionen Euro mit nach Hause zu nehmen, gilt es, eine knifflige Aufgabe zu lösen:

Jedes der 12 Mitglieder der Gruppe bekommt eine andere Nummer zwischen 1 und 12 zugeordnet. Auf einer Wand im Fernsehstudio sind zudem 12 Plättchen angebracht, die einerseits mit einer Nummer zwischen 1 und 12 beschriftet ist, hinter denen sich aber wiederum auch eine Nummer zwischen 1 und 12 verbirgt. Jedes Mitglied der Gruppe soll nun nacheinander zur Wand gehen und darf unter 6 Plättchen schauen. Nach jedem einzelnen Teilnehmer wird die Wand wieder in den ursprünglichen Zustand versetzt.

 

Der Jackpot wird nur geknackt, wenn alle Gruppenmitglieder ihre zugeteilte Nummer unter einem der 6 von ihnen aufgedeckten Plättchen finden.

Die anderen Mitglieder der Gruppe können von ihrem Platz aus nicht sehen, welche Plättchen umgedreht werden und welche Nummern sich dahinter verbergen. Nachdem ein Teilnehmer an der Reihe war wird er auf die andere Seite der Wand geführt, damit keine weitere Absprache mit seinen Gruppenkollegen möglich ist. Die Gruppenteilnehmer dürfen sich allerdings vorher absprechen um eine Strategie auszuklügeln, die ihre Gewinnchancen erhöht.

1.    Wie groß ist die Wahrscheinlichkeit, dass die Gruppe das Spiel gewinnt, wenn sich die Mitglieder nicht absprechen?

2.   Es gibt Strategien, mit denen die Gewinnwahrscheinlichkeit über die reine Ratewahrscheinlichkeit erhöht werden kann. Wie kann eine solche Strategie aussehen? Was macht diese Strategie zu einer, die die Erfolgsaussichten der Teilnehmer erhöht?

 

----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

August 2015: Summe 1000
Aus den Ziffern von 0 bis 9 können Sie verschiedene Mengen natürlicher Zahlen bilden, wobei jede Ziffer genau einmal verwendet wird, zum Beispiel: {347, 256, 9, 810} oder {12, 34, 56, 78, 90} oder {1, 23, 456, 7890}.

  a) Finden Sie eine Menge, bei der die Summe aller Zahlen 1000 ergibt.
  b) Ist die Menge unter den gegebenen Voraussetzungen eindeutig? Begründen Sie.

----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Juli 2015: Platten verlegen
Ein Bürogebäude ist in Büros von vier Metern Breite und fünf Metern Länge aufgeteilt. Aus Gründen der Statik stehen dabei in jedem Büro Säulen mit einem quadratischen Querschnitt. Diese Quadrate sind jeweils einen halben Meter breit. Die Säulen stehen je nach Büro an unterschiedlichen Stellen. Nun müssen die Decken der Büros neu mit Deckenplatten ausgelegt werden. Diese sind rechteckig, mit einer Breite von einem halben Meter und einer Länge von einem Meter. Die Decken zweier Büros sind in der folgenden Abbildung zu sehen.
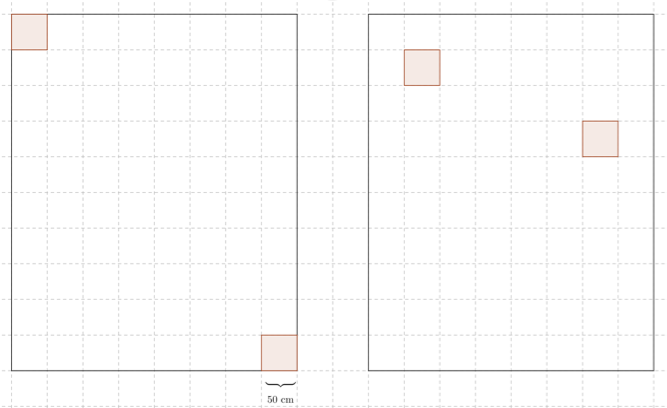1. Welche der beiden oben abgebildeten Decken kann man mit den Platten auslegen, ohne eine davon zersägen zu müssen?

2. Es kommen noch viele andere Säulenanordnungen vor, allerdings stets auf einem quadratischen Raster wie in der Abbildung. Bei welchen Anordnungen muss nicht gesägt werden?
 

 

----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Juni 2015: Zwei Mathe-Professoren unterhalten sich.
Der erste berichtet: "Ich hatte beim Tag der offenen Tür leider nur drei Besucher in meinem Knobelkurs, aber die waren pfiffig. Wir haben die Zeit genutzt und ein wenig Denksport betrieben. In der Summe waren die drei genauso alt wie Du. Das Produkt ihrer jeweiligen Alter ergab 2450. Wie alt waren die drei?"

Der zweite antwortet: "Dir ist schon klar, dass ich das nicht eindeutig beantworten kann?" "Stimmt", ergänzt der erste, "ich sollte dir noch verraten, dass alle drei jünger waren als unser Dekan." "Dann ist es einfach", sagt der zweite.

Wie alt ist der Dekan?

----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Mai 2015: Auf der Kippe
In der folgenden Abbildung sehen wir den Ausschnitt einer unendlich großen Fläche mit quadratischen Feldern.

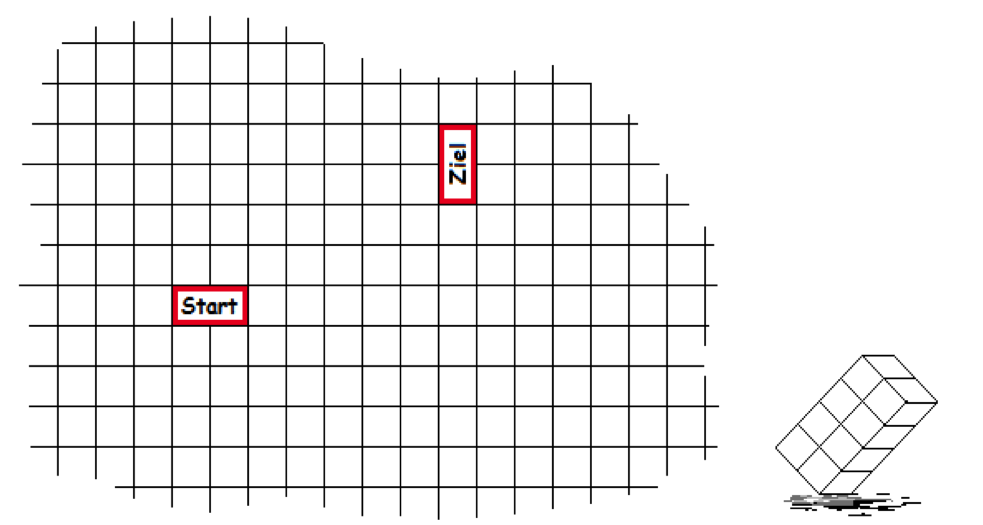
Außerdem haben wir einen Quader mit den Maßen 1x2x4 (Einheiten entsprechen den Seitenlängen der Feldquadrate). Der Quader steht "aufrecht" auf der Start-Fläche und soll allein durch Kippen auf die Ziel-Fläche gebracht werden. Dort soll er wieder "aufrecht" stehen. Folgende Aufgabe gilt es in diesem Monat zu lösen:

Bestimmen Sie eine Kippvorschrift, wie Sie den 1×2×4 Quader von der Start zur Ziel Fläche bekommen.
Gibt es für jede beliebige Position der Start und Ziel Flächen eine Kippvorschrift, sodass Sie den 1×2×4 Quader immer von der Start zur Ziel Fläche bringen können? – Begründen Sie Ihre Antwort.
Wir begrenzen die Fläche auf 10×15 Felder. Wie wirkt sich dies auf die „Beweglichkeit“ des Quaders aus?
Gelten die Regeln aus Teil b) auch für einen allgemeinen X×Y×Z Quader?

----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

April 2015: Die Blattlausplage
Marie liebt Pflanzen. In ihrem Garten wachsen auf 64 quadratischen Beeten Blumen. Die Beete sind in einem 8x8-Quadrat angeordnet. Unglücklicherweise sind sie von Blattläusen befallen. Da Marie umweltfreundlich ist, möchte sie Marienkäfer gegen die Blattlausplage einsetzen. Sie weiß aus Erfahrung, dass Marienkäfer ein neues Beet besiedeln, wenn auf mindestens zwei der angrenzenden* Beete schon Marienkäfer leben.

Was ist die kleinste Anzahl von Beeten, auf die Marie Mariekäfer setzen muss, damit am Ende auf allen Beeten Marienkäfer leben und Blattläuse fressen?
Auf welche Beete muss Marie die Marienkäfer setzen?

Die Blumen von Maries bester Freundin Marianne leiden auch unter der Blattlausplage. Marianne hat ihre Beete im gleichen Muster angeordnet wie Marie, allerdings sind ihre Beete in einem nxm-Gitter und nicht in einem Quadrat angeordnet. Marie weiß aber nicht, wie viele Beete Marianne hat.

 
Wie lässt sich die Lösung auf den Fall von nxm-Beeten verallgemeinern?
Was ist die benötigte Minimalzahl an Marienkäfern? Wie müssen diese gesetzt werden?
Weisen Sie nach, dass man keinesfalls mit weniger Marienkäfern auskommt!

 

---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

März 2015:
Das sogenannte isoperimetrische Problem gibt es in verschiedenen Varianten. So ist Ihnen vermutlich bekannt, dass unter allen Vierecken gleichen Umfangs das Quadrat maximalen Flächeninhalt besitzt. Im Problem des Monats soll eine etwas weniger bekannte Aussage bewiesen werden.

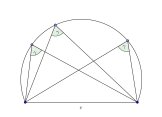
Wir betrachten alle Dreiecke mit einer gegebenen Seitenlänge c und einem gegebenen gegenüberliegenden Winkel γ. Mit etwas Probieren (z. B. mit GeoGebra) findet man leicht ein Dreieck mit maximalem Umfang. Der Beweis dafür, dass dieses ausgemachte Dreieck unter allen oben beschriebenen Dreiecken den größten Umfang besitzt, soll hier erbracht werden, und zwar ohne Verwendung von Werkzeugen aus der Analysis wie beispielsweise der Ableitung.

----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

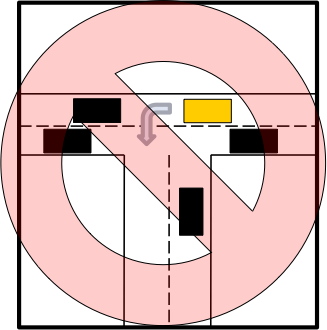
Februar 2015: Fido passt auf!
Diebstahl in der Nachbarschaft ist ein bewegendes und stets topaktuelles Thema. Selbst Bierkästen werden immer häufiger Opfer von Räubern. Deswegen muss Bierbrauer Karl um seine Existenz fürchten und beschließt zu kämpfen. Damit von seinem Gelände weniger gestohlen wird legt er sich den Wachhund Fido zu. Sein Brauhof hat die Form eines Quadrates von 25 Meter Seitenlänge. Genau in der Mitte steht eine quadratische Hundehütte mit großzügigen 5 Metern Kantenlänge. Fido ist an einer 10 Meter langen Leine an dieser der Hundehütte angeleint. Der Eingang zur Hütte ist niedriger als Fidos Schulterhöhe, wenn er steht. Wie viele Quadratmeter der Brauhoffläche bleiben durch Fido nach dieser Maßnahme noch immer mindestens ungeschützt?
Hauptgewinn: Benedikt Markus Anlauf
Kreativpreis: Daniel Barth
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Januar 2015: Die Homerplage auf dem Planeten Doughnut
Im Gegensatz zu unserer Erde ist der Planet Doughnut nicht kugel- sondern torusförmig, er sieht also aus wie ein riesiger Kringel. Die Einwohner haben ihre Heimat in 1024 x 1024 Parzellen unterteilt, in denen jeweils eine Familie lebt. Man kann auf kariertem Papier mit der entsprechenden Kästchenzahl einen Atlas dieser Welt zeichnen. Bewegt man sich auf diesem Atlas über den linken Rand hinaus, gelangt man, wie auf der Erde an den rechten Rand und umgekehrt. Im Gegensatz zur Erde funktioniert das aber auch mit dem oberen und unteren Rand.

Leider hat einer der Bewohner ein gefährliches Wesen namens Homer eingeschleppt. Dieses Wesen ist extrem gefräßig und pflanzt sich sehr schnell fort. So werden innerhalb eines Tages aus einem Homer vier, die sich noch am selben Tag in die Nachbarparzellen aller vier Himmelsrichtungen ausbreiten. Trifft dort ein Homer auf einen anderen, so fressen sie sich glücklicherweise gegenseitig auf.
Und hier nun die zu lösenden Fragen:
1. Wird sich die Homerplage jemals von selbst lösen?
2. Falls ja, wie lange wird das dauern?
3. Welche Bedeutung hat die Anzahl 1024 x 1024 der Parzellen in
   diesem Zusammenhang?

(Quellenhinweis: In Anlehnung an: Nolte, M. (2008). Zur Förderung mathematisch besonders begabter Grundschulkinder im Rahmen des Prima-Projekts in Hamburg. In: C. Fischer, F. J. Minks, U. Westphal. Individuelle Förderung: Begabungen entfalten - Persönlichkeit entwickeln. Berlin: LIT-Verlag, S. 46-60.)
Hauptgewinn: Daniel Wahlers
Kreativpreis: Sebastian Kahl

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Dezember 2014:
Gegeben ist eine natürliche Zahl n. Gesucht sind Rechenaufgaben, die folgende Kriterien erfüllen:
Es müssen alle Zahlen von 1 bis n verwendet werden.
Es darf nur + und - gerechnet werden.
Das Ergebnis der Aufgabe muss 0 oder 1 sein.
Beispiele für derartige Rechenaufgaben:  7+3-1-6+4-5-2=0          5+2-4-3+1=1
Wie findet man zu gegebenem n eine derartige Aufgabe?

(Quellenhinweis: In Anlehnung an: Ziegler, Günter M. (2004). Digitaler Adventskalender 2004. Neues aus Zellularien, S. 6-8.)
Hauptgewinn: Matthias Buttgereit
Kreativpreis: Andreas Rohe