Project P4
Project description
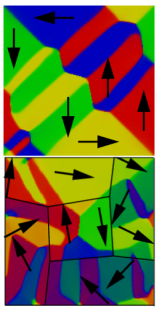
Investigation of size effects in ferroelectric materials by use of phase field simulations
The macroscopic material behavior of ferroelectric materials is closely connected to the temporal evolution of the microstructure. While grain boundaries are viewed as stationary, the configuration of ferroelectric domains is subject to significant change. This is for instance the case when an initially macroscopically unpoled crystal is poled by the application of an electric field: The local polarization will align itself with the electric field so that the crystal is then electrically poled and has piezoelectric properties.
The project centers around the simulation of domain structures as well as their temporal evolution. For this purpose a phase field model is adopted in which the polarization is taken as the order parameter. The temporal evolution of the order parameter due to the time-dependent Ginzburg-Landau equation determines the local material properties responsible for the effective material behavior. The phase field model consists of the coupled field problem of the mechanical and electrostatic equilibrium conditions besides the nonlinear evolution equation for the order parameter. The equations are implemented for the 2d case in the FE code FEAP, which allows for a flexible handling of boundary conditions and order parameter-dependent material constants.
The aim of the project is the numerical simulation of domain structures at inner and outer boundaries. For that purpose some basic relationships are developed on the basis of 2d simulations, which are then more closely investigated for the 3d case. At first the existing model is extended to allow for the application of Robin boundary conditions for the order parameter. Subsequently a study of domain configurations for different boundary conditions in the vicinity of cracks is carried out, and the implications for different fracture mechanical parameters are assessed. Furthermore the influence on the domain structure of a variety of transition conditions at grain boundaries in the context of varying grain size is considered. Finally some of the aspects addressed are further analyzed by means of 3d simulations.
Publications
| Keip, M.-A., Schrade, D., Thai, H., Schröder, J., Svendsen, B., Müller, R. & Gross, D. (2015), "Coordinate-invariant phase-field modeling of ferroelectrics, part II: Model formulation and single-crystal simulations", GAMM-Mitteilungen. Vol. 38(1), pp. 115-131. |
BibTeX:
@article{Keip2015,
author = {Keip, M.-A. and Schrade, D. and Thai, H. and Schröder, J. and Svendsen, B. and Müller, R. and Gross, D.},
title = {Coordinate-invariant phase-field modeling of ferroelectrics, part II: Model formulation and single-crystal simulations},
journal = {GAMM-Mitteilungen},
year = {2015},
volume = {38},
number = {1},
pages = {115--131}
}
|
| Schrade, D., Keip, M.-A., Thai, H., Schröder, J., Svendsen, B., Müller, R. & Gross, D. (2015), "Coordinate-invariant phase-field modeling of ferroelectrics, part I: Model formulation and single-crystal simulations", GAMM-Mitteilungen. Vol. 38(1), pp. 102-114. |
BibTeX:
@article{Schrade2015,
author = {Schrade, D. and Keip, M.-A. and Thai, H. and Schröder, J. and Svendsen, B. and Müller, R. and Gross, D.},
title = {Coordinate-invariant phase-field modeling of ferroelectrics, part I: Model formulation and single-crystal simulations},
journal = {GAMM-Mitteilungen},
year = {2015},
volume = {38},
number = {1},
pages = {102--114},
note = {P4, P1, P6}
}
|
| Schrade, D., Müller, R., Gross, D., Keip, M.-A., Thai, H. & Schröder, J. (2014), "An invariant formulation for phase field models in ferroelectrics", International Journal of Solids and Structures. Vol. 51, pp. 2144-2156. |
BibTeX:
@article{Schrade2014,
author = {Schrade, D. and Müller, R. and Gross, D. and Keip, M.-A. and Thai, H. and Schröder, J.},
title = {An invariant formulation for phase field models in ferroelectrics},
journal = {International Journal of Solids and Structures},
year = {2014},
volume = {51},
pages = {2144--2156},
note = {P4, P1}
}
|
| Schrade, D., Müller, R. & Gross, D. (2014), "Phase field modeling in ferroelectric materials in the context of size effects", Proceedings of the Second Seminar on the Mechanics of Multifunctional Materials. , pp. 83-86. |
BibTeX:
@article{Schrade2014a,
author = {Schrade, D. and Müller, R., and Gross, D.},
title = {Phase field modeling in ferroelectric materials in the context of size effects},
journal = {Proceedings of the Second Seminar on the Mechanics of Multifunctional Materials},
year = {2014},
pages = {83--86},
note = {P4}
}
|
| Schrade, D., Müller, R., Gross, D. & Steinmann, P. (2014), "Phase field simulations of the poling behavior of BaTiO$_3$ nano-scale thin films with SrRuO$_3$ and Au electrodes", European Journal of Mechanics - A/Solids. Vol. 49, pp. 455-466. |
BibTeX:
@article{Schrade2014b,
author = {Schrade, D. and Müller, R. and Gross, D. and Steinmann, P.},
title = {Phase field simulations of the poling behavior of BaTiO$_3$ nano-scale thin films with SrRuO$_3$ and Au electrodes},
journal = {European Journal of Mechanics - A/Solids},
year = {2014},
volume = {49},
pages = {455--466},
note = {DOI: 10.1016/j.euromechsol.2014.08.007 P4 and P5}
}
|
| Schrade, D., Müller, R. & Gross, D. (2014), "Untersuchung von Größeneffekten in ferroelektrischen Materialen für multiferroische Komposite", GAMM-Rundbrief. |
BibTeX:
@article{Schrade2014c,
author = {Schrade, D. and Müller, R. and Gross, D.},
title = {Untersuchung von Größeneffekten in ferroelektrischen Materialen für multiferroische Komposite},
journal = {GAMM-Rundbrief},
year = {2014},
note = {P4}
}
|
| Schrade, D., Müller, R. & Gross, D. (2014), "Phase field modeling in ferroelectric materials in the context of size effects", Proceedings in Applied Mathematics and Mechanics. , pp. 443-444. |
BibTeX:
@article{Schrade2014d,
author = {Schrade, D. and Müller, R., and Gross, D.},
title = {Phase field modeling in ferroelectric materials in the context of size effects},
journal = {Proceedings in Applied Mathematics and Mechanics},
year = {2014},
pages = {443--444},
note = {P4}
}
|
| Schrade, D., Müller, R. & Gross, D. (2014), "Phase field modeling in ferroelectric materials in the context of size effects", Proceedings of the 5th International Congress on Computational Mechanics and Simulation, Chennai 2014. , pp. 83-86. |
BibTeX:
@article{Schrade2014e,
author = {Schrade, D. and Müller, R., and Gross, D.},
title = {Phase field modeling in ferroelectric materials in the context of size effects},
journal = {Proceedings of the 5th International Congress on Computational Mechanics and Simulation, Chennai 2014},
year = {2014},
pages = {83--86},
note = {P4}
}
|
| Schrade, D., Müller, R. & Gross, D. (2013), "On the physical interpretation of material parameters in phase field models for ferroelectrics", Archive of Applied Mechanics. Vol. 83, pp. 1393-1412. |
BibTeX:
@article{Schrade2013,
author = {Schrade, D. and Müller, R. and Gross, D.},
title = {On the physical interpretation of material parameters in phase field models for ferroelectrics},
journal = {Archive of Applied Mechanics},
year = {2013},
volume = {83},
pages = {1393--1412},
note = {P4}
}
|
Stand: 12.05.2015
Latest results
Initially the existing phase field model was extended to account for the anisotropic elastic and dielectric properties of BaTiO_3. This was achieved by means of an invariant formulation for transverse isotropy. The enhanced model was used for the simulation of thin layers with SrRuO_3 und Au electrodes, the focus being on size effects regarding the coercive fields and remanent polarizations. Furthermore, size effects concerning the configurational force at the crack tip of cracked single crystals were investigated. This was done for different electrical and mechanical crack flank conditions. Another study focussed on the microstructure evolution in single and polycrystals of different sizes. The observed size effects are reflected in the poling behavior of the investigated polycrystals. Morover, the influence of a decoupled order parameter along the grain boundaries of a polycrystal was investigated. For future simulations the phase field model has been extended to the 3D case.



