Project P5
Project description

Adaptivly smoothed molecular static methods for the simulation of ferroelectric materials
Ferroelectric materials are modeled and simulated on different length scales between the electron structure and the continuum description. Moreover models and algorithms have been developed further in the last decade and attain accurate results on the atomistic level. Still the computational costs of the established Methods are significant. For that reason atomistic scale simulation methods will be further developed in the future.
The goal of this project is the development and investigation of adaptivly smoothed molecular static methods for the multiscale analysis of electromechanical phenomena in ferroelectric materials. On the one hand an accurate description of the material on an atomistic scale has to be made to investigate relevant regions such as domain walls. On the other hand ferroelectric structures should be simulated on a technically relevant scale with mechanical and electrical loads based on atomistic methods.
In order to simulate ferroelectric materials on the micro scale, ab initio methods and molecular dynamics have been used for some time. Yet, not only the small length scale is a limiting factor but also the time step length. Through the use of molecular static methods the dynamic problem shall be transferred to a quasi-static algorithm. Furthermore multiscale methods such as the quasicontinuum-method, which is a hybrid of molecular statics and the finite element method, shall be analyzed.
In addition to the targeted methodological outcome, the results shall be compared directly to the other projects which use non-atomistc methods for the simulation of ferroelectric materials.
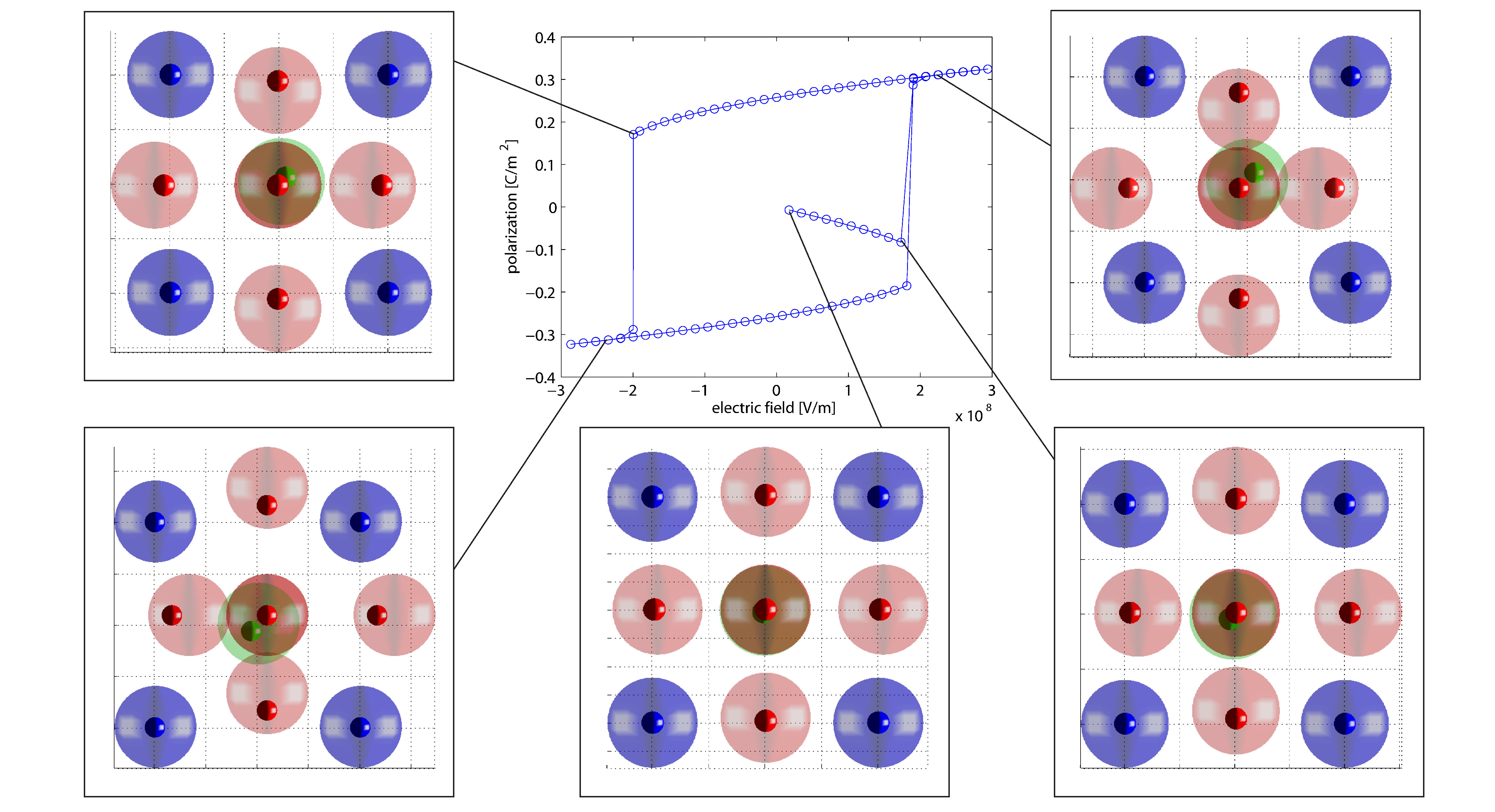
Dielectric hysteresis loop of ferroelectric barium titanate
Publications
| Endres, F. & Steinmann, P. (2014), "Molecular statics simulations of head to head and tail to tail nanodomains of rhombohedral barium titanate", Computational Materials Science. Vol. 97, pp. 20-25. |
BibTeX:
@article{Endres2014,
author = {Endres, F. and Steinmann, P.},
title = {Molecular statics simulations of head to head and tail to tail nanodomains of rhombohedral barium titanate},
journal = {Computational Materials Science},
year = {2014},
volume = {97},
pages = {20--25},
note = {P5 DOI: 10.1016/j.commatsci.2014.10.001}
}
|
| Endres, F. & Steinmann, P. (2014), "Molecular static simulations of ferroelectric material hysteresis behaviour", Proceedings in Applied Mathematics and Mechanics. Vol. 14, pp. 409-410. |
BibTeX:
@article{Endres2014a,
author = {Endres, F. and Steinmann, P.},
title = {Molecular static simulations of ferroelectric material hysteresis behaviour},
journal = {Proceedings in Applied Mathematics and Mechanics},
year = {2014},
volume = {14},
pages = {409--410},
note = {P5}
}
|
| Endres, F. & Steinmann, P. (2013), "On molecular statics simulation of ferroelectric barium titanate", Proceedings in Applied Mathematics and Mechanics. Vol. 13, pp. 313-314. |
BibTeX:
@article{Endres2014c,
author = {Endres, F. and Steinmann, P.},
title = {On molecular statics simulation of ferroelectric barium titanate},
journal = {Proceedings in Applied Mathematics and Mechanics},
year = {2013},
volume = {13},
pages = {313--314},
note = {P5}
}
|
| Endres, F. & Steinmann, P. (2014), "An extended molecular statics algorithm simulating the electromechanical continuum response of ferroelectric materials", Computational Mechanics. Vol. 51, pp. 2144-2156. |
BibTeX:
@article{EndSte:CM,
author = {Endres, F. and Steinmann, P.},
title = {An extended molecular statics algorithm simulating the electromechanical continuum response of ferroelectric materials},
journal = {Computational Mechanics},
year = {2014},
volume = {51},
pages = {2144--2156},
note = {DOI: 10.1007/s00466-014-1072-7 P5}
}
|
| Keip, M.-A., Steinmann, P. & Schröder, J. (2014), "Two-scale computational homogenization of electroelasticity at finite strains", Computer Methods in Applied Mechanics and Engineering. Vol. 278, pp. 62-79. |
BibTeX:
@article{Keip2104,
author = {M.-A. Keip and P. Steinmann and J. Schröder},
title = {Two-scale computational homogenization of electroelasticity at finite strains},
journal = {Computer Methods in Applied Mechanics and Engineering},
year = {2014},
volume = {278},
pages = {62--79}
}
|
| Schrade, D., Müller, R., Gross, D. & Steinmann, P. (2014), "Phase field simulations of the poling behavior of BaTiO3 nano-scale thin films with SrRuO3 and Au electrodes", European Journal of Mechanics - A/Solids. Vol. 49, pp. 455-466. |
BibTeX:
@article{Schrade2014b,
author = {Schrade, D. and Müller, R. and Gross, D. and Steinmann, P.},
title = {Phase field simulations of the poling behavior of BaTiO3 nano-scale thin films with SrRuO3 and Au electrodes},
journal = {European Journal of Mechanics - A/Solids},
year = {2014},
volume = {49},
pages = {455-466},
note = {DOI: 10.1016/j.euromechsol.2014.08.007 P4 and P5}
}
|
| Endres, F. & Steinmann, P. (2014), "On an atomistic scale finite element method for the simulation of ferroelectric functional materials", Proceedings of the 2nd Seminar on The Mechanics of Multifunctional Materials. (12), pp. 17-20. |
BibTeX:
@article{Endres2014b,
author = {Endres, F. and Steinmann, P.},
title = {On an atomistic scale finite element method for the simulation of ferroelectric functional materials},
journal = {Proceedings of the 2nd Seminar on The Mechanics of Multifunctional Materials},
year = {2014},
number = {12},
pages = {17--20},
note = {P5}
}
|
| Endres, F. & Steinmann, P. (2015), "Molecular statics simulations of ferroelectric barium titanate in the rhombohedral phase", GAMM Mitteilung. Vol. 38(1), pp. 132-146. |
BibTeX:
@article{Endres2015,
author = {Endres, F. and Steinmann, P.},
title = {Molecular statics simulations of ferroelectric barium titanate in the rhombohedral phase},
journal = {GAMM Mitteilung},
year = {2015},
volume = {38},
number = {1},
pages = {132--146},
note = {P5}
}
|
Stand: 14.05.2015
Latest results
In the first phase of the research project a new molecular statics algorithm for the simulation of ferroelectric materials has been developed and implemented. Furthermore, the algorithm has been used to simulate different fundamental questions on the atomistic length scale. The new developed algorithm also considers the residual stresses of a discrete particle system. Thus, a macroscopic continuum deformation of a discrete particle system caused by residual stresses is calculated. Therefore, it is possible to not only calculate the dielectric hysteresis of a ferroelectric crystal but also the butterfly hysteresis based on an atomistic simulation.
The algorithm has already been used to study size effects of head to head and tail to tail domain walls of barium titanate. Furthermore, the impact of residual stresses on 90° domain walls have been determined. The results show that macroscopic residual stresses cause the typical laminar structures of 90° domain walls since the potential energies are lower compared to homogenous polarized mono domains. Thus, the results of this research project not only predict material behavior on the atomistic length scale but also help understanding material behavior in general.
The simulation of ferroelectric materials improved rapidly over the last decades. Especially particle based methods rendered substantial progress. Reasons for these improvements are not only caused by increased CPU power but also based on the development of simulation models. Nevertheless the gap in simulated length scales between macroscopic, continuum mechanics approaches and atomistic simulations, e.g. molecular dynamics (MD), is still significant. Especially the applied energy potentials which consider long range interactions increase the computational effort of MD simulations of ferroelectric materials. Furthermore MD simulations require very small time steps which also increase the calculation time.

In order to reduce the computational effort of atomistic simulations a molecular static finite element algorithm has been implemented. Due to the significant reduction of computational costs it is possible to calculate the dielectric hysteresis behavior of a crystal and the mechanical stress and strain response of a ferroelectric atomist lattice. As a result not only the piezoelectric effect but also the inverse piezoelectric effect can be calculated on an atomistic scale. This is a major advantage compared to MD simulation since most MD algorithms require a constant volume over time. There are methods, e.g. the Parrinello-Rahman method, which allow a simulation box to change the size and shape due to external or internal stresses. Nevertheless these methods increase the computational costs of MD simulations significantly.
The developed algorithm can be used to calculate phenomena, e.g. domain walls and boundary effects. Such simulations not only predict the behavior of material but also help understanding ferroelectric material in general. Furthermore the calculation of phenomena, like domain walls can be used to develop continuum mechanical approaches, e.g. phase field simulations, further. Especially knowledge of domain wall energies and mechanical stress at domain walls can help to increase the accuracy of continuum mechanical models.