Subproject
Advanced Finite Element Modelling of 3D Crack Propagation by a Phase Field Approach
JP Dr.-Ing. Charlotte Kuhn (Kaiserslautern),
Prof. Dr.-Ing. Ralf Müller (Kaiserslautern)
Abstract
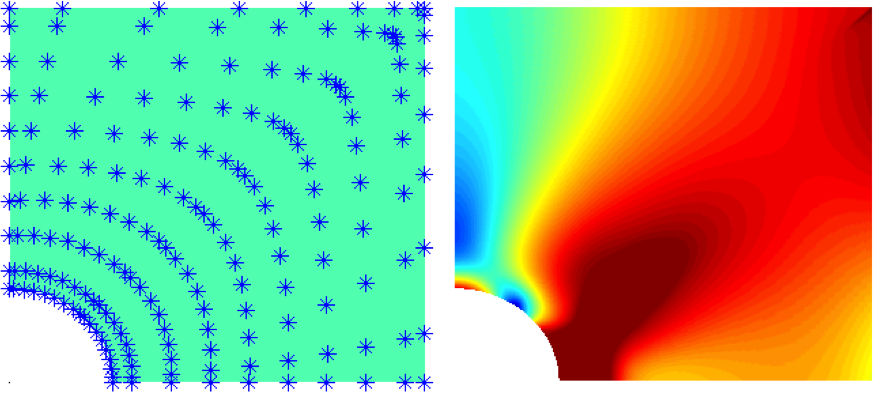
The main aim of the project is to establish a robust and efficient numerical implementation of a fracture phase field model exploiting the numerical efficiency of so called exponential shape functions. Motivated by preliminary 1d analyses shape functions of exponential character are developed. These special shape functions satisfy standard requirements for finite element shape functions such as the interpolation property, and the partition of unity. Similar to the incorporation of the square root behaviour of the displacements at the crack tip in the extended finite element method (XFEM), exponential shape functions incorporate the regularization length scale of the phase field model and the exponential character of the 1d analytic solution of the evolution equation into the discretization resulting in a superior approximation behaviour. In contrast to XFEM approaches, no nodal enrichment is required therefore. Due to the incorporation of the phase field length scale into the shape functions and the need for a proper orientation of the exponential elements, this new type of approximation requires special numerical treatment and analysis. So far the applicability of the approach is limited to rather simple 2d problems with a priori known crack paths due to a lack of adaptivity with respect to the evolving fracture field. In order to generalize the approach, adaptive integration and orientation schemes for the exponential shape functions are developed for 2d and 3d problems. In addition dynamic fracture problems are considered with help of the newly developed adaptive exponential shape functions.