Subproject
Isogeometric and stochastic collocation methods for nonlinear probabilistic multiscale problems in solid mechanics
Prof. Dr.-Ing. Laura De Lorenzis(Braunschweig)
Prof. Dr. Hermann G. Matthies (Braunschweig)
Dr. Joachim Rang (Braunschweig)
Frederik Fahrendorf, M. Sc. (Braunschweig)
Abstract
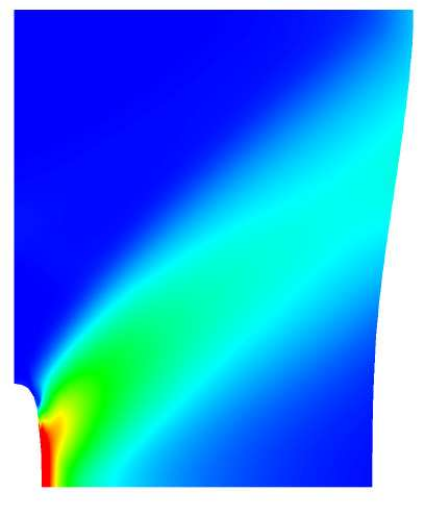
In this project, we intend to use the newly developed concept of isogeometric collocation (IGA-C) in combination with stochastic collocation (SC) to achieve stable and computationally efficient higher-order modeling of irreversible multiscale behavior in solid mechanics. The basic assumption is that the microstructure of a heterogeneous solid is uncertain and hence should be modeled probabilistically. In order to describe the effects of the microscale uncertainty not only on the mean macroscopic fields, but also on their variability, a probabilistic treatment of the scale transition is also needed. As the computational cost of such stochastic computations may be orders of magnitude higher than that of simple deterministic analyses, an unprecedented computational efficiency is sought in the combination of IGA-C for the mechanical/deterministic modeling, and of an SC scheme with novel ansatz functions for the stochastic discretization. The numerical framework to be developed encompasses local and nonlocal elasticity and plasticity with finite strains, as well as contact, damage and fracture models.