Subproject
Abstract
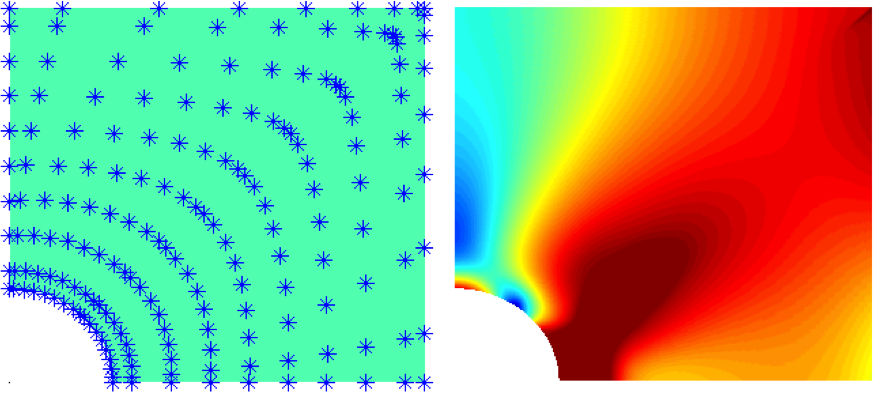
The aim of this project is to establish reliable and efficient numerical methods for models of solids with spatial discontinuities caused by the evolution of dissipative processes such as plastification, damage or fracture. In particular, the project focuses on such prototypical models that use the class of BV-functions to mathematically describe the discontinuities, that are guaranteed to converge to a solution of the infinite-dimensional model and for which iterative solution methods can be constructed. Emphasis is on unregularized numerical approaches that lead to sharp approximations of discontinuities on coarse grids and rigorous convergence proofs. The main objectives of the research project are the development, analysis, and implementation of finite element methods for model problems describing discontinuities in BV. Particular focus is on the improvement of existing a priori estimates and the analysis of adaptive finite element methods, especially the derivation of efficiency estimates for a primal-dual gap estimator and deduction of quasi-optimality, for BV-prototype models such as the (bilaterally constrained) Rudin-Osher-Fatemi image denoising model. Moreover, the project aims at the derivation of a priori and a posteriori error estimates and the construction of time-space adaptive finite element methods for time-dependent BV-model problems. The techniques will be transferred to analytically justified and closely related models for the description of rate-independent/rate-dependent processes, in particular delamination, damage and fracture. The methods and results will be applied and transferred to particular model scenarios and benchmark problems in mechanics.