Subproject
Robust and Efficient Finite Element Discretizations for Higher-Order Gradient Formulations
Prof. Dr.-Ing. Daniel Balzani (Bochum)
JProf. Dr. Mira Schedensack (Münster)
Abstract
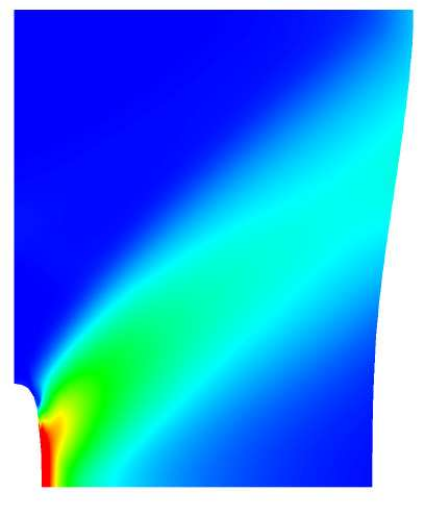
The simulation of challenging engineering problems, including, e.g., a softening material behavior or geometrical singularities, requires robust numerical discretization methods. More and more, nonlocal approaches including higher-order derivatives are considered in order to, e.g., capture a length-scale dependent material response or to cure mesh-dependent solutions. This modeling approach poses new challenges with view to their algorithmic treatment since classical methods are not directly applicable. This is due to the higher-order derivatives taken into account which induce a switch from a second-order to a fourth-order partial differential equation (PDE), which leads to complicated ansatz functions in the approximation. This project defines novel robust and reliable formulations and discretizations for gradient elasticity and gradient damage. The gradient of the displacements will be the only independent variable using standard Lagrange basis functions. This enables the implementation of the new discretizations in existing software packages and leads to an efficient approximation of the solution. The key idea is to characterize derivatives as rotation-free functions. Besides the introduction of new formulations and suitable discretizations, the proposal focuses on the error analysis, the implementation, the computations of benchmark problems and the comparison of the new discretizations with existing ones. Furthermore the project will develop an a posteriori error analysis and thereby devise efficient and reliable error estimators. Those are utilized to drive automatic mesh-adaptive algorithms that are indispensable for exploiting the existing computer power.