Subproject
Foundation and application of generalized mixed FEM towards nonlinear problems in solid mechanics
Abstract
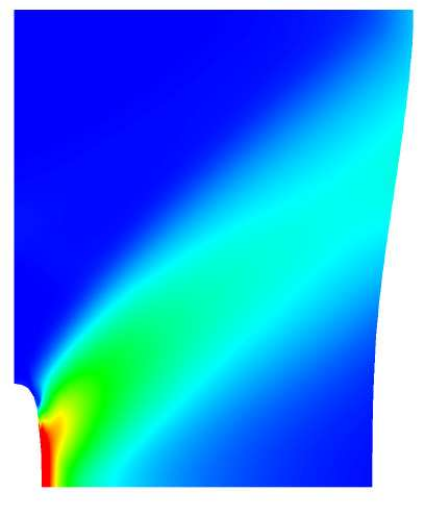
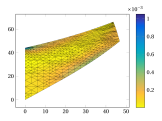
The research of this project aims at the effective and reliable simulation in nonlinear continuum mechanics with development of adaptive non-standard methods based on ultraweak formulations between
nonconforming, mixed and discontinuous Petrov-Galerkin (dPG) Finite Element Methods. Recent breakthroughs in the dPG methodology for nonlinear problems motivate the application of adaptive dPG schemes with built-in error control to further problems such as hyperelasticity, the obstacle problem and time-evolving elastoplasticity. Optimal convergence rates of adaptive nonlinear LS and dPG methods and Arnold-Winther FEM and guaranteed error estimation for dPG methods involving explicit constants and correct scaling will be investigated.